Question

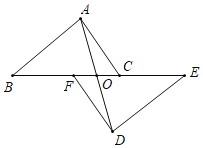
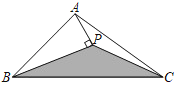
【题目】如图，BP平分∠ABC，AP⊥BP，垂足为P，连接CP，若三角形△ABC内有一点M，则点M落在△BPC内（包括边界）的概率为_____．

Answer 1

【答案】

【解析】

延长AP交BC于E，据已知条件证得△ABP≌△EBP，根据全等三角形的性质得到AP＝PE，得出S△ABP＝S△EBP，S△ACP＝S△ECP，推出S△PBC＝S△ABC，根据概率公式可得的答案．

延长AP交BC于E，

∵BP平分∠ABC，

∴∠ABP＝∠EBP，

∵AP⊥BP，

∴∠APB＝∠EPB＝90°，

在△ABP和△EBP中，

，

∴△ABP≌△EBP（ASA），

∴AP＝PE，

∴S△ABP＝S△EBP，S△ACP＝S△ECP，

∴S△PBC＝S△ABC，

∴点M落在△BPC内（包括边界）的概率=＝．

故答案为．