题目内容
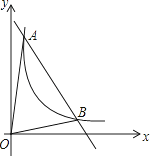
如图,一次函数y=kx+b与反比例函数y=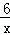 (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<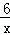 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
解:(1)∵点A(m,6),B(3,n)两点在反 比例函数y=
比例函数y=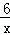 (x>0)的图象上,
(x>0)的图象上,
∴m=1,n=2,
即A(1,6),B(3,2).
又∵点A(m,6),B(3,n)两点在一次函数y=kx+b的图象上,
∴ .
.
解得 ,
,
则该一次函数的解析式为:y=﹣2x+3;
(2)根据图象可知使kx+b< 成立的x的取值范围是0<x<1或x>2;
成立的x的取值范围是0<x<1或x>2;
(3)分别过点A、B作AE⊥x轴,BC⊥x轴,垂足分别是E、C点.直线AB交x轴于D点.
令﹣2x+8=0,得x=4,即D(4,0).
∵A(1,6),B(3,2),
∴AE=6,BC=2,
∴S△AOB=S△AOD﹣S△BOD= ×4×6﹣
×4×6﹣ ×4×2=8.
×4×2=8.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案陆地上最高处是珠穆朗玛峰顶,高出海平面8848m,记为+8848m;陆地上最低处是地处亚洲西部的死海,低于海平面约415m,记为( )
|
| A. | +415m | B. | ﹣415m | C. | ±415m | D. | ﹣8848m |
如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
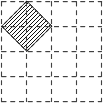
|
| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
如图是一个螺母的示意图,它的俯视图是( )

|
| A. |
| B. |
| C. |
| D. |
|
在▱ABCD中,AB=10,BC=14,E,F分别为边BC,AD上的点,若四边形AECF为正方形,则AE的长为( )
|
| A. | 7 | B. | 4或10 | C. | 5或9 | D. | 6或8 |
 •(m﹣n),其中
•(m﹣n),其中 =2.
=2.




 ;
;
 的中点.若∠A=40°,则∠B= 度.
的中点.若∠A=40°,则∠B= 度.