Question

图1和图2中，优弧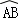所在⊙O的半径为2，AB=2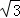．点P为优弧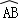上一点（点P不与A，B重合），将图形沿BP折叠，得到点A的对称点A′．

（1）点O到弦AB的距离是　 　，当BP经过点O时，∠ABA′=　 　°；

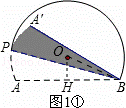
（2）当BA′与⊙O相切时，如图2，求折痕的长：

（3）若线段BA′与优弧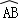只有一个公共点B，设∠ABP=α．确定α的取值范围．

Answer 1

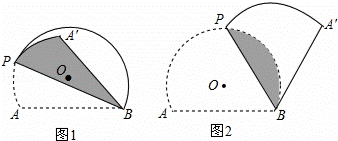
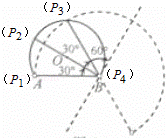
       解：（1）①过点O作OH⊥AB，垂足为H，连接OB，如图1①所示．

∵OH⊥AB，AB=2，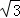

∴AH=BH=．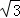

∵OB=2，

∴OH=1．

∴点O到AB的距离为1．

②当BP经过点O时，如图1②所示．

∵OH=1，OB=2，OH⊥AB，

∴sin∠OBH==．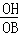

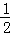∴∠OBH=30°．

由折叠可得：∠A′BP=∠ABP=30°．

∴∠ABA′=60°．

故答案为：1、60．

（2）过点O作OG⊥BP，垂足为G，如图2所示．

∵BA′与⊙O相切，

∴OB⊥A′B．

∴∠OBA′=90°．

∵∠OBH=30°，

∴∠ABA′=120°．

∴∠A′BP=∠ABP=60°．

∴∠OBP=30°．

∴OG=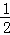OB=1．

∴BG=．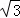

∵OG⊥BP，

∴BG=PG=．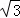

∴BP=2．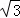

∴折痕的长为2．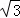

（3）∵点P，A不重合，∴α＞0°，

由（1）得，当α增大到30°时，点A′在上，

∴当0°＜α＜30°时，点A′在⊙O内，线段BA′与只有一个公共点B．

由（2）知，α增大到60°时，BA′与⊙O相切，即线段BA′与只有一个公共点B．

当α继续增大时，点P逐渐靠近B点，但点P，B不重合，

∴∠OBP＜90°．

∵α=∠OBA+∠OBP，∠OBA=30°，

∴α＜120°．

∴当60°＜α＜120°时，线段BA′与只有一个公共点B．

综上所述：线段BA′与优弧只有一个公共点B时，α的取值范围是0°＜α＜30°或60°≤α＜120°．