Question

如图，二次函数y=ax²+bx的图象与一次函数y=x+2的图象交于A、B两点，点A的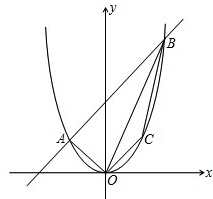横坐标是-1，点B的横坐标是2．
（1）求二次函数的表达式；
（2）设点C在二次函数图象的OB段上，求四边形OABC面积的最大值．

Answer 1

解：（1）把x=-1和2分别代入y=x+2，得到y的值分别是1、4，因而A、B的坐标分别是（-1，1），（2，4）．
根据题意得到：
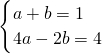
解得
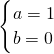
因而二次函数的解析式是y=x²．

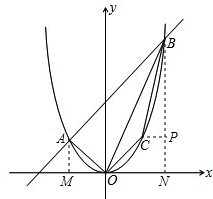
（2）过点A、B作AM⊥x轴，BN⊥x轴，分别交于M、N．过点C作CP⊥BN于P．
设C的坐标是（x，y）．
梯形AMNB的面积=（AM+BN）•MN=（1+4）×3=；
△AOM的面积=AM•OM=；
△BCP的面积=CP•BP=（2-x）（4-y）=（2-x）（4-x²）；
四边形CPNO的面积是（CP+ON）•PN=[（2-x）+2]•y=（4-x）•x²．
因而四边形OABC面积s=梯形AMNB的面积-△AOM的面积-△BCP的面积-四边形CPNO的面积=-x²+2x+3．
当x=1时，函数s=-x²+2x+3有最大值是4．
分析：（1）把x=-1和2分别代入y=x+2，就可以求出A，B的坐标，把这两点的坐标代入二次函数的解析式，就可以求出二次函数的解析式．
（2）过点A、B作AM⊥x轴，BN⊥x轴，分别交于M、N．过点C作CP⊥BN于P．设P的坐标是（x，y）．因而四边形OABC面积就可以表示成x的函数，根据函数的性质，就可以求出四边形OABC面积的最大值．
点评：本题主要考查了待定系数法求函数的解析式，求面积的最值问题一般要转化为函数的最值问题，依据函数的性质解决．