题目内容
4. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则$\frac{AP}{PB}$的值=3,tan∠APD的值=2.
如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则$\frac{AP}{PB}$的值=3,tan∠APD的值=2.
分析 首先连接BE,由题意易得BF=CF,△ACP∽△BDP,然后由相似三角形的对应边成比例,易得DP:CP=1:3,即可得PF:CF=PF:BF=1:2,在Rt△PBF中,即可求得tan∠BPF的值,继而求得答案.
解答 解:∵四边形BCED是正方形,
∴DB∥AC,
∴△DBP∽△CAP,
∴$\frac{AP}{PB}$=$\frac{AC}{DB}$=3,
连接BE,
∵四边形BCED是正方形,
∴DF=CF=$\frac{1}{2}$CD,BF=$\frac{1}{2}$BE,CD=BE,BE⊥CD,
∴BF=CF,
根据题意得:AC∥BD,
∴△ACP∽△BDP,
∴DP:CP=BD:AC=1:3,
∴DP:DF=1:2,
∴DP=PF=$\frac{1}{2}$CF=$\frac{1}{2}$BF,
在Rt△PBF中,tan∠BPF=$\frac{BF}{PF}$=2,
∵∠APD=∠BPF,
∴tan∠APD=2,
故答案为:3,2.
点评 此题考查了相似三角形的判定与性质与三角函数的定义.此题难度适中,解题的关键准确作出辅助线,注意转化思想与数形结合思想的应用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
14.下列函数中,满足y的值随x的值增大而增大的是( )
| A. | y=-2x | B. | y=3x-1 | C. | y=$\frac{1}{x}$ | D. | y=x2 |
15.下列调查中,最适合采用全面调查(普查)的是( )
| A. | 对重庆市居民日平均用水量的调查 | |
| B. | 对一批LED节能灯使用寿命的调查 | |
| C. | 对重庆新闻频道“天天630”栏目收视率的调查 | |
| D. | 对某校九年级(1)班同学的身高情况的调查 |
12.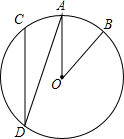 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=40°,则∠ADC的度数是( )| A. | 40° | B. | 30° | C. | 20° | D. | 15° |
19.若$\sqrt{a-1}$+b2-4b+4=0,则ab的值等于( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
16.函数y=$\frac{1}{x+2}$中,x的取值范围是( )
| A. | x≠0 | B. | x>-2 | C. | x<-2 | D. | x≠-2 |

 无解,且使关于x的分式方程
无解,且使关于x的分式方程  有整数解,那么所有满足条件的a值的和是( ).
有整数解,那么所有满足条件的a值的和是( ).