题目内容
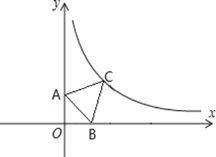
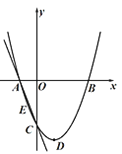
【题目】如图,抛物线![]() 的图象经过点C(0,-2),顶点D的坐标为(1,
的图象经过点C(0,-2),顶点D的坐标为(1,![]() ),与
),与![]() 轴交于A、B两点.
轴交于A、B两点.
(1)求抛物线的解析式.
(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和![]() 的值.
的值.
(3)点F(0,![]() )是
)是![]() 轴上一动点,当
轴上一动点,当![]() 为何值时,
为何值时,![]() 的值最小.并求出这个最小值.
的值最小.并求出这个最小值.
(4)点C关于![]() 轴的对称点为H,当
轴的对称点为H,当![]() 取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)E
;(2)E![]() ,
,![]() ;(3)当
;(3)当![]() 时,
时,![]() 有最小值为
有最小值为![]() ;(4)存在,点Q的坐标为
;(4)存在,点Q的坐标为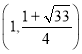 或
或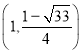 或
或![]() 或
或![]() .
.
【解析】
(1)把C、D坐标代入二次函数解析式,列方程组求出a、c的值即可;(2)根据抛物线解析式可求出A、B两点坐标,即可求出AC、AB的长,设直线AC的解析式为:![]() ,把A、C坐标代入可求出k、b的值,可得直线AC的解析式,根据△AOC∽△AEB可得
,把A、C坐标代入可求出k、b的值,可得直线AC的解析式,根据△AOC∽△AEB可得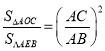 ,可求出△AEB的面积,进而可求出
,可求出△AEB的面积,进而可求出![]() ,代入直线AC解析式可求出E点坐标,根据相似三角形的性质即可求出
,代入直线AC解析式可求出E点坐标,根据相似三角形的性质即可求出![]() 的值;(3)连接BF,过点F作FG⊥AC于G,可得FG=
的值;(3)连接BF,过点F作FG⊥AC于G,可得FG=![]() ,可得当折线段BFG与BE重合时,取得最小值,由(2)可知∠ABE=∠ACO,利用∠ABE的余弦和正切求出BE的长和
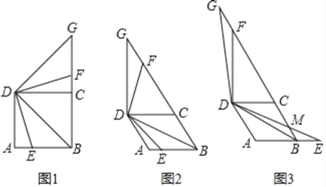
,可得当折线段BFG与BE重合时,取得最小值,由(2)可知∠ABE=∠ACO,利用∠ABE的余弦和正切求出BE的长和 ![]() 的值即可;(4)可分如下三种情况:当点Q为直角顶点时(如图):由(3)可知F点的坐标,根据点C与点H关于
的值即可;(4)可分如下三种情况:当点Q为直角顶点时(如图):由(3)可知F点的坐标,根据点C与点H关于![]() 轴对称可求出点H坐标,设Q(1,
轴对称可求出点H坐标,设Q(1,![]() ),过点Q作QM
),过点Q作QM![]()
![]() 轴于点M,可得Rt△QHM∽Rt△FQM,即可证明
轴于点M,可得Rt△QHM∽Rt△FQM,即可证明![]() ,即可求出m的值;当点H为直角顶点时,可得HQ//x轴,即可得出Q点坐标,当点F为直角顶点时,可得FQ//x轴,即可求出Q点坐标.
,即可求出m的值;当点H为直角顶点时,可得HQ//x轴,即可得出Q点坐标,当点F为直角顶点时,可得FQ//x轴,即可求出Q点坐标.
(1)∵![]() 的图象经过点C(0,-2),顶点D的坐标为(1,
的图象经过点C(0,-2),顶点D的坐标为(1,![]() ),
),
∴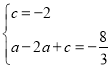 ,
,
解得: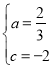 ,
,
∴抛物线解析式为:![]() .
.
(2)∵抛物线解析式为:![]() .
.
∴当y=0时,![]() =0,
=0,
解得:x1=-1,x2=3,
∴OA=1,OB=3,AB=4,
∵C(0,-2),
∴OC=2,
∴AC=![]() ,
,
设直线AC的解析式为:![]() ,则
,则![]()
解得:![]()
∴直线AC的解析式为:![]()
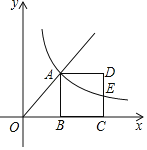
当△AOC∽△AEB时(如图)
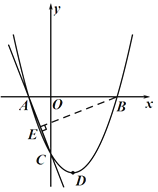
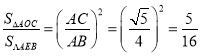
∵![]()
∴![]()
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴E![]() ,
,
∵△AOC∽△AEB,
∴![]() ,
,
∴![]() ,
,
(3)如图,连接BF,过点F作FG⊥AC于G
则FG=![]() ,
,
∴![]() ,
,
当折线段BFG与BE重合时,取得最小值,
由(2)可知∠ABE=∠ACO,
∴![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() 有最小值为
有最小值为![]() .
.

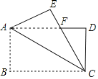
(4)可分如下三种情况:
①当点Q为直角顶点时(如图):
由(3)得F![]() ,
,
∵C(0,-2),
∴H(0,2),
∵点Q在抛物线的对称轴上,
∴设Q(1,![]() ),
),
过点Q作QM![]()
![]() 轴于点M,
轴于点M,
则Rt△QHM∽Rt△FQM,
∴![]() ,
,
∴![]() ,
,
即![]()
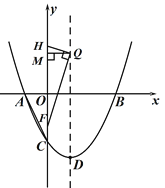
∴Q(1,![]() )或Q(1,
)或Q(1,![]() ),
),
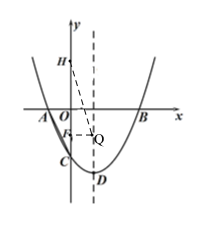
②如图,当点H为直角顶点时:
∵∠FHQ=90°,
∴HQ//x轴,
∵H(0,2),Q点在抛物线对称轴上,
∴Q(1,2),
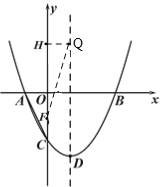
③如图,当点F为直角顶点时,
∵∠HFQ=90°,
∴FQ//x轴,
∵F(0,![]() ),Q点在抛物线对称轴上,
),Q点在抛物线对称轴上,
∴Q(1,![]() ).
).
综上所述,点Q的坐标为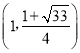 或
或 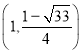 或
或 ![]() 或
或![]()