Question

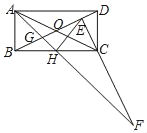
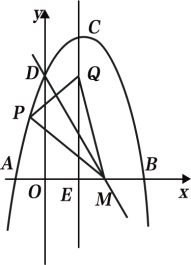
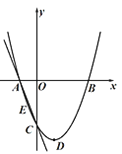
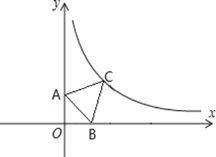
【题目】如图所示，△ABC为等边三角形，点A的坐标为（0，4），点B在x轴上，点C在反比例函数的图象上，则点B的坐标为__________．

Answer 1

【答案】（，0）

【解析】

首先根据点C是反比例函数（x＞0）图象上一点，设点C的坐标为，设点B的坐标为（a，0），则AB的中点D的坐标为；然后证明△AED∽△DFC，根据，列出关于a、x的方程组，解方程组即可求出当△ABC是等边三角形时，点B的坐标为多少即可．

如图，过点C作CD⊥AB于点D，CG⊥OB于G，过D点作EF∥OB，交y轴于E，交CG于F，

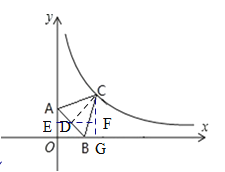
设点C的坐标为，点B的坐标为（a，0），

∵△ABC是等边三角形，

∴D为AB的中点，

∴CD⊥AB，

∵；

∵CD⊥AB，

∴∠ADE+∠CDF=90°，

∵∠ADE+∠DAE=90°，

∴∠DAE=∠CDF，

∵∠AED=∠CFD=90°，

∴△AED∽△DFC，

∴，

即，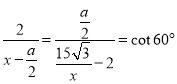

整理，可得，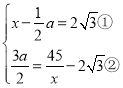

由①②，解得，（舍去），

∴当△ABC是等边三角形时，点B的坐标为：（，0）．

故答案为：（，0）