题目内容
在△ABC中,若c=4,b=7,BC边上的中线AD=
,则边长a= .
| 7 |
| 2 |
考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:
分析:因为cos∠ADB=-coc∠ADC,所以可设BD=DC=x,在△ABD和△ACD中,分别利用余弦定理可得x2+(
)2-42=-(x2+(
)2-72),解得x=
,所以BC=9,即a=9.
| 7 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
解答:解:∵∠ADB+∠ADC=180°,
∴cos∠ADB=-coc∠ADC
设BD=DC=x,在△ABD和△ACD中,
分别利用余弦定理可得x2+(
)2-42=-(x2+(
)2-72),
解得x=
.
所以BC=9,即a=9.
∴cos∠ADB=-coc∠ADC
设BD=DC=x,在△ABD和△ACD中,
分别利用余弦定理可得x2+(
| 7 |
| 2 |
| 1 |
| 2 |
解得x=
| 9 |
| 2 |
所以BC=9,即a=9.
点评:本题主要考查余弦定理的应用,解题的关键是利用cos∠ADB=-coc∠ADC结合余弦定理得出方程.

练习册系列答案
相关题目
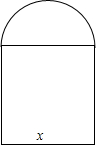 如图,隧道横截面的下部是矩形,上部是半圆,周长为20m.
如图,隧道横截面的下部是矩形,上部是半圆,周长为20m. 观察如图规律,则第100行的左起第一位数字是
观察如图规律,则第100行的左起第一位数字是