题目内容
7.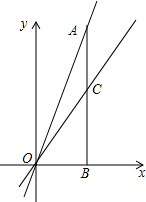 如图,已知A、C的坐标分别是A(m,n)、C(m,a),连接AC交x轴于B点,若3S△AOC=2S△BOC,则n与a之间的数量关系是n=$\frac{5}{3}$a.
如图,已知A、C的坐标分别是A(m,n)、C(m,a),连接AC交x轴于B点,若3S△AOC=2S△BOC,则n与a之间的数量关系是n=$\frac{5}{3}$a.
分析 首先求得AC=n-a,BC=m,进一步利用三角形的面积分别求得△AOC和△BOC的面积代入3S△AOC=2S△BOC,得出n与a之间的数量关系即可.
解答 解:∵A、C的坐标分别是A(m,n)、C(m,a),
∴AC=n-a,BC=a,
∴S△AOC=$\frac{1}{2}$m(n-a),S△BOC=$\frac{1}{2}$ma,
∵3S△AOC=2S△BOC,
∴$\frac{1}{2}$m(n-a)×3=$\frac{1}{2}$ma×2,
即n=$\frac{5}{3}$a.
故答案为:n=$\frac{5}{3}$a.
点评 本题考查了两条直线相交或平行的问题,两条直线的交点坐标,三角形的面积,根据点的坐标求得AC是解决问题的关键.

练习册系列答案
相关题目

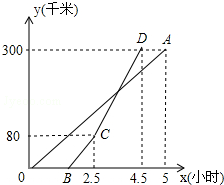 如图,一辆货车和一辆轿车先后从甲地向乙地行驶.线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
如图,一辆货车和一辆轿车先后从甲地向乙地行驶.线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题: