题目内容
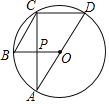
【题目】如图,点![]() 是
是![]() 的内心,
的内心,![]() 的延长线和
的延长线和![]() 的外接圆圆
的外接圆圆![]() 相交于点
相交于点![]() ,过
,过![]() 作直线
作直线![]() .
.
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求优弧
,求优弧![]() 的长.
的长.

【答案】(1)见解析;(2)优弧![]() 的长=
的长=![]() .
.
【解析】
(1)连接OD交BC于H,如图,利用三角形内心的性质得到∠BAD=∠CAD,则![]() ,利用垂径定理得到OD⊥BC,BH=CH,从而得到OD⊥DG,然后根据切线的判定定理得到结论;
,利用垂径定理得到OD⊥BC,BH=CH,从而得到OD⊥DG,然后根据切线的判定定理得到结论;
(2)连接BD、OB,如图,先证明∠DEB=∠DBE得到DB=DE=6,再利用正弦定义求出∠BDH=60°,则可判断△OBD为等边三角形,所以∠BOD=60°,OB=BD=6,则∠BOC=120°,然后根据弧长公式计算优弧![]() 的长.
的长.
(1)证明:连接![]() 交
交![]() 于
于![]() ,如图,
,如图,

∵点![]() 是
是![]() 的内心,
的内心,
∴![]() 平分
平分![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是圆
是圆![]() 的切线;
的切线;
(2)解:连接![]() 、
、![]() ,如图,
,如图,
∵点![]() 是
是![]() 的内心,
的内心,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴优弧![]() 的长=
的长=![]() .
.

练习册系列答案
相关题目
【题目】某超市计划购进甲、乙两种商品,两种商品的进价、售价如下表:
商品 | 甲 | 乙 |
进价(元/件) |
|
|
售价(元/件) | 200 | 100 |
若用360元购进甲种商品的件数与用180元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价是多少元?
(2)若超市销售甲、乙两种商品共50件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完50件甲、乙两种商品的总利润为
),设销售完50件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.