题目内容
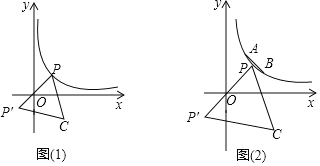
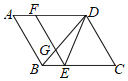
【题目】如图1,AD、BD分别是![]() 的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.
的内角∠BAC、∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E.

(1)求证:![]() ;
;
(2)如图2,如果AE=AB,且BD:DE=2:3,求BC:AB的值;
(3)如果∠ABC是锐角,且![]() 与
与![]() 相似,求∠ABC的度数,并直接写出
相似,求∠ABC的度数,并直接写出![]() 的值.
的值.
【答案】(1)详见解析;(2)![]() ;(3)∠ABC=30°或者∠ABC=45°,
;(3)∠ABC=30°或者∠ABC=45°,![]() 或者
或者![]()
【解析】
(1)先根据题意证明![]() 以及
以及![]() ,再适当变形即可得到答案;
,再适当变形即可得到答案;
(2)先根据角平分线的性质和直线平行的性质证明△BAF≌△CAF,再根据全等三角形的性质得到BF=CF,再根据BD:DE=2:3,计算即可得到答案;
(3)根据△ABC与△ADE相似,∠DAE=90°,因此△ABC中必有一个内角为90°,再根据∠ABC是锐角,得到∠ABC≠90°,再分情况讨论即可得到答案;
(1)证明:如图1中,
∵AE⊥AD,
∴∠DAE=90°,∠E=90°-∠ADE,
∵AD平分∠BAC,
∴![]() ,
,
同理可得:![]() ,
,
∴![]()
![]() ,
,
![]()
(2)解:延长AD交BC于点F.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD,
∵AB=AE,
∴∠ABE=∠E,
BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠E=∠CBE,
∴AE∥BC,
∴∠AFB=∠EAD=90°,![]()
∴∠AFB=∠AFC=90°,
在△BAF和△CAF中,

∴△BAF≌△CAF(ASA),
∴BF=CF(全等三角形对应边相等),
∵BD:DE=2:3
∴![]() ,
,
∴![]() ;
;
(3) ∵△ABC与△ADE相似,∠DAE=90°,
∴△ABC中必有一个内角为90°
∵∠ABC是锐角,
∴∠ABC≠90°.
①当∠BAC=∠DAE=90°时,
∵![]() (由(1)知),
(由(1)知),
∵∠ABC+∠C=90°,
∴∠ABC=30°,
∴此时![]() ,
,
②当∠C=∠DAE=90°时,![]() ,
,
∴∠EDA=45°,
∵△ABC与△ADE相似,
∴∠ABC=45°,
此时![]() ,
,
综上,∠ABC=30°或者∠ABC=45°,![]() 或者
或者![]() ;
;

 期末集结号系列答案
期末集结号系列答案