题目内容
已知:Rt△ABC的三边长均为整数,点A(4,0),B(0,3).若点C在第一象限内且在反比例函数 的图象上,则k的值为________.
的图象上,则k的值为________.
12, ,
,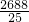 ,
,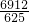
分析:如果求出了C点的坐标,那么只需将C点的坐标代入反比例函数的解析式 ,即可求出k的值.由于AB=5,所以当Rt△ABC的三边长均为整数时,分AB为斜边和AB为直角边进行讨论:①如果AB=5为斜边,那么两条直角边分别为3,4.当AC=3时,易求C(4,3);当BC=3时,根据直角三角形的性质及三角函数的定义,可求出C(
,即可求出k的值.由于AB=5,所以当Rt△ABC的三边长均为整数时,分AB为斜边和AB为直角边进行讨论:①如果AB=5为斜边,那么两条直角边分别为3,4.当AC=3时,易求C(4,3);当BC=3时,根据直角三角形的性质及三角函数的定义,可求出C( ,
, );②如果AB=5为直角边,那么另外两条边分别为12,13.当AC=12时,根据相似三角形的判定与性质可求C(
);②如果AB=5为直角边,那么另外两条边分别为12,13.当AC=12时,根据相似三角形的判定与性质可求C( ,
, );当BC=12时,根据相似三角形的判定与性质可求C(
);当BC=12时,根据相似三角形的判定与性质可求C( ,
,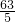 ).
).
解答: 解:∵A(4,0),B(0,3),
解:∵A(4,0),B(0,3),
∴OA=4,OB=3,
∵∠AOB=90°,
∴AB=5.
分两种情况:
①如果AB=5为斜边,那么两条直角边分别为3,4.
当AC=3时,则BC=4,C1点坐标为(4,3),
所以k=4×3=12;
当BC=3时,设AC2与BC1交于点P,过点C2作C2D⊥BC1于D.
由AAS易证△BPC2≌△APC1,则BP=AP,PC2=PC1.
设PC1=x,则AP=BP=4-x,
在△APC1中,由勾股定理,
得x2+32=(4-x)2,解得x= .
.
则AP=BP= ,
,
∴BD=BC2•cos∠C2BD=BC2•cos∠C1AP=3×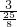 =
= ,C2D=BC2•sin∠C2BD=BC2•sin∠C1AP=3×
,C2D=BC2•sin∠C2BD=BC2•sin∠C1AP=3×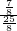 =
=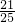 ,
,
∴OB+C2D=3+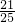 =
= ,
,
 ∴C2点坐标为(
∴C2点坐标为( ,
, ),
),
∴k= ×
× =
=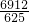 ;
;
②如果AB=5为直角边,那么另外两条边分别为12,13.
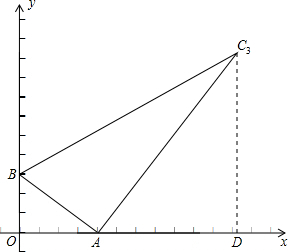
当AC=12时,∠BAC=90°.过点C3作C3D⊥x轴于D.
∵∠C3DA=∠AOB=90°,∠C3AD=∠ABO=90°-∠OAB,
∴△C3DA∽△AOB,
∴C3D:AO=DA:OB=C3A:AB,
即C3D:4=DA:3=12:5,
∴C3D= ,DA=
,DA= ,
,
∴OD=OA+AD=4+ =
= ,
,
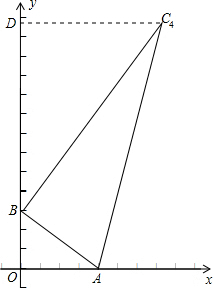 ∴C3点坐标(
∴C3点坐标( ,
, ),
),
∴k= ×
× =
=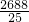 ;
;
当BC=12时,∠ABC=90°.过点C4作C4D⊥y轴于D.
∵∠C4DB=∠BOA=90°,∠C4BD=∠OAB=90°-∠ABO,
∴△C4DB∽△BOA,
∴C4D:BO=DB:OA=C4B:BA,
即C4D:3=DB:4=12:5,
∴C4D= ,DB=
,DB= ,
,
∴OD=OB+BD=3+ =
=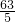 ,
,
∴C4点坐标( ,
,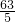 ),
),
∴k= ×
×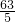 =
= .
.
综上可知,k的值为12, ,
,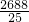 ,
,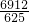 .
.
故答案为:12, ,
,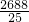 ,
,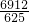 .
.
点评:本题考查了直角三角形的性质,相似三角形的判定与性质,勾股定理,解直角三角形,综合性较强,熟记常见的勾股数及将Rt△ABC分AB为斜边和AB为直角边进行讨论是解题的关键.
 ,
,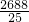 ,
,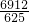
分析:如果求出了C点的坐标,那么只需将C点的坐标代入反比例函数的解析式
 ,即可求出k的值.由于AB=5,所以当Rt△ABC的三边长均为整数时,分AB为斜边和AB为直角边进行讨论:①如果AB=5为斜边,那么两条直角边分别为3,4.当AC=3时,易求C(4,3);当BC=3时,根据直角三角形的性质及三角函数的定义,可求出C(
,即可求出k的值.由于AB=5,所以当Rt△ABC的三边长均为整数时,分AB为斜边和AB为直角边进行讨论:①如果AB=5为斜边,那么两条直角边分别为3,4.当AC=3时,易求C(4,3);当BC=3时,根据直角三角形的性质及三角函数的定义,可求出C( ,
, );②如果AB=5为直角边,那么另外两条边分别为12,13.当AC=12时,根据相似三角形的判定与性质可求C(
);②如果AB=5为直角边,那么另外两条边分别为12,13.当AC=12时,根据相似三角形的判定与性质可求C( ,
, );当BC=12时,根据相似三角形的判定与性质可求C(
);当BC=12时,根据相似三角形的判定与性质可求C( ,
,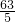 ).
).解答:
 解:∵A(4,0),B(0,3),
解:∵A(4,0),B(0,3),∴OA=4,OB=3,
∵∠AOB=90°,
∴AB=5.
分两种情况:
①如果AB=5为斜边,那么两条直角边分别为3,4.
当AC=3时,则BC=4,C1点坐标为(4,3),
所以k=4×3=12;
当BC=3时,设AC2与BC1交于点P,过点C2作C2D⊥BC1于D.
由AAS易证△BPC2≌△APC1,则BP=AP,PC2=PC1.
设PC1=x,则AP=BP=4-x,
在△APC1中,由勾股定理,
得x2+32=(4-x)2,解得x=
 .
.则AP=BP=
 ,
,∴BD=BC2•cos∠C2BD=BC2•cos∠C1AP=3×
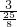 =
= ,C2D=BC2•sin∠C2BD=BC2•sin∠C1AP=3×
,C2D=BC2•sin∠C2BD=BC2•sin∠C1AP=3×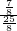 =
=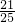 ,
,∴OB+C2D=3+
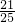 =
= ,
, ∴C2点坐标为(
∴C2点坐标为( ,
, ),
),∴k=
 ×
× =
=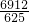 ;
;②如果AB=5为直角边,那么另外两条边分别为12,13.
当AC=12时,∠BAC=90°.过点C3作C3D⊥x轴于D.
∵∠C3DA=∠AOB=90°,∠C3AD=∠ABO=90°-∠OAB,
∴△C3DA∽△AOB,
∴C3D:AO=DA:OB=C3A:AB,
即C3D:4=DA:3=12:5,
∴C3D=
 ,DA=
,DA= ,
,∴OD=OA+AD=4+
 =
= ,
,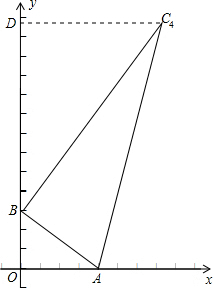 ∴C3点坐标(
∴C3点坐标( ,
, ),
),∴k=
 ×
× =
=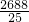 ;
;当BC=12时,∠ABC=90°.过点C4作C4D⊥y轴于D.
∵∠C4DB=∠BOA=90°,∠C4BD=∠OAB=90°-∠ABO,
∴△C4DB∽△BOA,
∴C4D:BO=DB:OA=C4B:BA,
即C4D:3=DB:4=12:5,
∴C4D=
 ,DB=
,DB= ,
,∴OD=OB+BD=3+
 =
=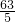 ,
,∴C4点坐标(
 ,
,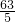 ),
),∴k=
 ×
×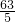 =
= .
.综上可知,k的值为12,
 ,
,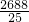 ,
,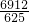 .
.故答案为:12,
 ,
,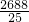 ,
,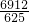 .
.点评:本题考查了直角三角形的性质,相似三角形的判定与性质,勾股定理,解直角三角形,综合性较强,熟记常见的勾股数及将Rt△ABC分AB为斜边和AB为直角边进行讨论是解题的关键.

练习册系列答案
相关题目
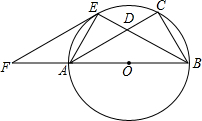 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.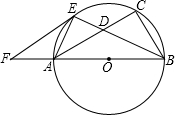 ∥AC交BA的延长线于F.
∥AC交BA的延长线于F.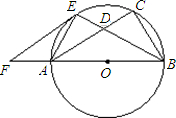 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交
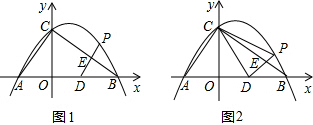 已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上,点D的坐标为(2,0).
已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上,点D的坐标为(2,0).