题目内容
如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C,∠DAB=∠B=30°.
【小题1】直线BD是否与⊙O相切?为什么?
【小题2】连接CD,若CD=5,求AB的长. 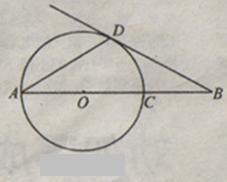
答:直线BD与⊙O相切.理由如下:
如图,连接OD,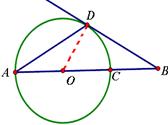

∵∠ODA=∠DAB=∠B=30°,
∴∠ODB=180°-∠ODA-∠DAB-∠B=180°-30°-30°-30°=90°,
即OD⊥BD,
∴直线BD与⊙O相切.
【小题1】由(1)知,∠ODA=∠DAB=30°,
∴∠DOB=∠ODA+∠DAB=60°,
又∵OC=OD,
∴△DOB是等边三角形,
∴OA=OD=CD=5.
又∵∠B=30°,∠ODB=30°,
∴OB=2OD=10.
∴AB=OA+OB=5+10=15.
解析【小题1】连接OD,通过计算得到∠ODB=90°,证明BD与⊙O相切.
【小题1】△OCD是边长为5的等边三角形,得到圆的半径的长,然后求出AB的长

练习册系列答案
相关题目
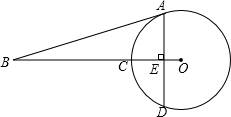
 25、如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C.∠DAB=∠B=30°.
25、如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C.∠DAB=∠B=30°. 如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C,直线BD与⊙O相切,∠DAB=30°.
如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C,直线BD与⊙O相切,∠DAB=30°. 如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C,∠DAB=∠B=30°.
如图,AD是⊙O的弦,AB经过圆心O,交⊙O于点C,∠DAB=∠B=30°.