题目内容
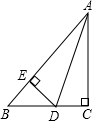 如图,△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于E,测得BC=9,BE=3,则△BDE的周长是
如图,△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于E,测得BC=9,BE=3,则△BDE的周长是考点:角平分线的性质
专题:
分析:由△ABC中,∠C=90°,AD平分∠BAC,过点D作DE⊥AB于E,根据角平分线的性质,即可得DE=CD,继而可求得△BDE的周长是:BE+BC,则可求得答案.
解答:解:∵△ABC中,∠C=90°,
∴AC⊥CD,
∵AD平分∠BAC,DE⊥AB,
∴DE=CD,
∵BC=9,BE=3,
∴△BDE的周长是:BE+BD+DE=BE+BD+CD=BE+BC=3+9=12.
故答案为12.
∴AC⊥CD,
∵AD平分∠BAC,DE⊥AB,
∴DE=CD,
∵BC=9,BE=3,
∴△BDE的周长是:BE+BD+DE=BE+BD+CD=BE+BC=3+9=12.
故答案为12.
点评:此题考查了角平分线的性质.此题比较简单,注意角平分线的性质:角平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目
2014年10月某日我国部分城市的最低气温如表(单位℃),由此可见其中最冷的城市是( )
| 城市 | 温州 | 嘉兴 | 北京 | 哈尔滨 | 广州 |
| 最低气温 | 20 | 17 | -8 | -15 | 25 |
| A、广州 | B、哈尔滨 | C、北京 | D、嘉兴 |
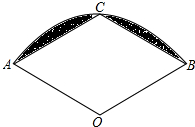 如图,在扇形AOB中,半径OA=1,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是
如图,在扇形AOB中,半径OA=1,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是