题目内容
古希腊的毕达哥拉斯学派由古希腊哲学家毕达哥拉斯所创立,毕达哥拉斯学派认为数是万物的本原,事物的性质是由某种数量关系决定的,如他们研究各种多边形数:记第n个k边形数N(n,k)=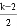 n2+
n2+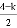 n(n≥1,k≥3,k、n都为整数),
n(n≥1,k≥3,k、n都为整数),
如第1个三角形数N(1,3)=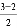 ×12+
×12+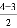 ×1=1;
×1=1;
第2个三角形数N(2,3)=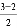 ×22+
×22+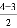 ×2=3;
×2=3;
第3个四边形数N(3,4)=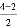 ×32+
×32+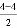 ×3=9;
×3=9;
第4个四边形数N(4,4)=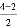 ×42+
×42+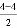 ×4=16.
×4=16.
(1)N(5,3)=________,N(6,5)=________;
(2)若N(m,6)比N(m+2,4)大10,求m的值;
(3)若记y=N(6,t)-N(t,5),试求出y的最大值.
(1)15;51;(2)7;(3)当t=5时,y有最大值,其最大值为16. 【解析】试题分析:(1)根据N(n,k)的定义,求出N(5,3),N(6,5)的值即可. (2)根据N(m,6)比N(m+2,4)大10,列出方程即可解决问题. (3)首先根据y=N(6,t)-N(t,5),构建二次函数,然后根据二次函数的性质即可解决问题. 试题解析:(1)N(5,3)=×52+×5 =...
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目


 x2﹣x与x轴交于点A,点P在抛物线上,连结AP.若△OAP是以OA为底边的等腰三角形,则△OAP的面积是_____.
x2﹣x与x轴交于点A,点P在抛物线上,连结AP.若△OAP是以OA为底边的等腰三角形,则△OAP的面积是_____.
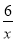 的图象上,若0<x2<x1,则y1、y2的大小关系是( )
的图象上,若0<x2<x1,则y1、y2的大小关系是( )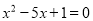 ;
; .
.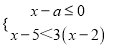 无解,且关于x的分式方程
无解,且关于x的分式方程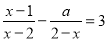 有整数解的概率为( )
有整数解的概率为( )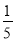 B.
B. 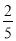 C.
C. 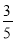 D.
D. 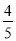
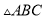 的顶点
的顶点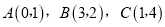 均在正方形网格的格点上.
均在正方形网格的格点上.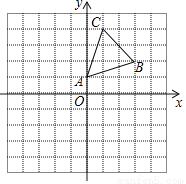
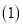 画出
画出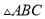 关于x轴的对称图形
关于x轴的对称图形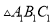 ;
;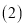 将
将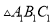 向左平移3个单位后得到
向左平移3个单位后得到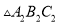 ,画出
,画出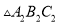 ,并写出顶点
,并写出顶点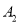 的坐标.
的坐标.