题目内容
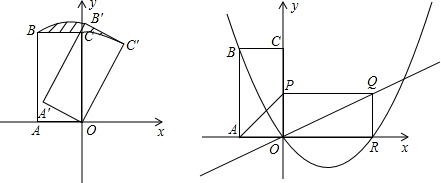
在平面直角坐标系中的矩形OABC.如图所示,点B的坐标是(-2,4).
(1)把矩形OABC绕点O顺时针方向旋转,使AB的对应边A′B′经过点C时,
①试求C′的坐标;
②求线段BC扫过的面积;
(2)把矩形OABC绕点O顺时针方向旋转90°得矩形OPQR,连接AP,作直线OQ和经过B,O,R,三点的抛物线.
①求抛物线和直线OQ的解析式;
②问能否在直线OQ上找到一点M,在抛物线上找到一点N,使以M,N,A,P为顶点的四边形是以AP为边的平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
(1)把矩形OABC绕点O顺时针方向旋转,使AB的对应边A′B′经过点C时,
①试求C′的坐标;
②求线段BC扫过的面积;
(2)把矩形OABC绕点O顺时针方向旋转90°得矩形OPQR,连接AP,作直线OQ和经过B,O,R,三点的抛物线.
①求抛物线和直线OQ的解析式;
②问能否在直线OQ上找到一点M,在抛物线上找到一点N,使以M,N,A,P为顶点的四边形是以AP为边的平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.

考点:二次函数综合题
专题:压轴题
分析:(1)过点C′作C′H⊥y轴于点H,连接OB,如图1.①运用三角函数及勾股定理即可求出∠COC′、C′H、OH,就可得到点C′的坐标;②只需运用割补法就可解决问题;
(2)①只需运用待定系数法就可求出抛物线和直线OQ的解析式;
②可设点M的坐标为(2m,m),将平行四边形分为两种情况(?APMN和?APNM)进行讨论,然后运用平移的方法得到点M与点N坐标之间的关系,从而得到点N的坐标为(2m-2,m-2)或(2m+2,m+2),然后将点N的坐标代入抛物线的解析式就可解决问题.
(2)①只需运用待定系数法就可求出抛物线和直线OQ的解析式;
②可设点M的坐标为(2m,m),将平行四边形分为两种情况(?APMN和?APNM)进行讨论,然后运用平移的方法得到点M与点N坐标之间的关系,从而得到点N的坐标为(2m-2,m-2)或(2m+2,m+2),然后将点N的坐标代入抛物线的解析式就可解决问题.
解答:解:(1)过点C′作C′H⊥y轴于点H,连接OB,如图1.
①由题可知:OA′=OA=2,OC′=OC=4,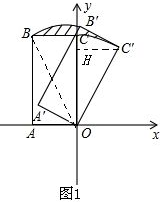
∠B′A′O=∠BAO=90°,∠A′OC′=∠AOC=90°.
在Rt△OA′C中,cos∠A′OC=
=
,
∴∠A′OC=60°,
∴∠COC′=30°.
∴C′H=
OC′=2,OH=
=2
,
∴点C′的坐标为(2,2
);
②由旋转不变性可得S△OC′B′=S△OCB,
∴S阴影=(S扇形OBB′+S△OC′B′)-(S扇形OCC′+S△OCB)
=S扇形OBB′-S扇形OCC′
=
-
=
(OB2-OC2)
=
BC2
=
×4
=
.
∴线段BC扫过的面积为
.
(2)①由旋转可得:OR=OC=4,QR=BC=2,
∴点R(4,0),点Q(4,2).
设抛物线的解析式为y=ax(x-4),
则有a×(-2)×(-2-4)=4,
解得:a=
,
∴抛物线的解析式为y=
x(x-4).
设直线OQ的解析式为y=kx,
则有4k=2,
解得k=
,
∴直线OQ的解析式为y=
x;
②设点M的坐标为(2m,m),
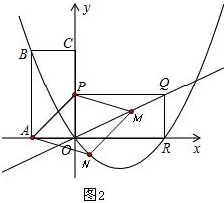
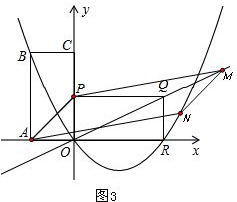
Ⅰ.若该平行四边形为?APMN,如图2、图3.
由于点A可由点P先向下平移两个单位再向左平移2个单位所得,
因此点N可由点M先向下平移两个单位再向左平移2个单位所得,
∴点N的坐标为(2m-2,m-2),
∵点N在抛物线y=
x(x-4)上,
∴
(2m-2)(2m-2-4)=m-2,
整理得:4m2-19m+18=0,
解得:m1=
,m2=
,
∴点M的坐标为(
,
)或(
,
);
Ⅱ.若该平行四边形为?APNM,如图4、图5.
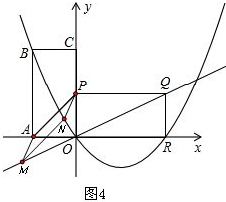
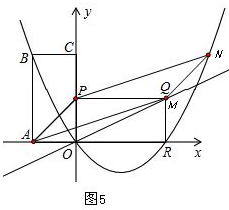
由于点P可由点A先向右平移两个单位再向上平移2个单位所得,
因此点N可由点M先向右平移两个单位再向上平移2个单位所得,
∴点N的坐标为(2m+2,m+2),
∵点N在抛物线y=
x(x-4)上,
∴
(2m+2)(2m+2-4)=m+2,
整理得:4m2-3m-10=0,
解得:m3=2,m4=-
,
∴点M的坐标为(4,2)或(-
,-
).
综上所述:符合条件的点M的坐标为:
(
,
)、(
,
)、(4,2)、(-
,-
).
①由题可知:OA′=OA=2,OC′=OC=4,

∠B′A′O=∠BAO=90°,∠A′OC′=∠AOC=90°.
在Rt△OA′C中,cos∠A′OC=
| OA′ |
| OC |
| 1 |
| 2 |
∴∠A′OC=60°,
∴∠COC′=30°.
∴C′H=
| 1 |
| 2 |
| 42-22 |
| 3 |
∴点C′的坐标为(2,2
| 3 |
②由旋转不变性可得S△OC′B′=S△OCB,
∴S阴影=(S扇形OBB′+S△OC′B′)-(S扇形OCC′+S△OCB)
=S扇形OBB′-S扇形OCC′
=
| 30πOB2 |
| 360 |
| 30πOC2 |
| 360 |
=
| π |
| 12 |
=
| π |
| 12 |
=
| π |
| 12 |
=
| π |
| 3 |
∴线段BC扫过的面积为
| π |
| 3 |
(2)①由旋转可得:OR=OC=4,QR=BC=2,
∴点R(4,0),点Q(4,2).
设抛物线的解析式为y=ax(x-4),
则有a×(-2)×(-2-4)=4,
解得:a=
| 1 |
| 3 |
∴抛物线的解析式为y=
| 1 |
| 3 |
设直线OQ的解析式为y=kx,
则有4k=2,
解得k=
| 1 |
| 2 |
∴直线OQ的解析式为y=
| 1 |
| 2 |
②设点M的坐标为(2m,m),
Ⅰ.若该平行四边形为?APMN,如图2、图3.


由于点A可由点P先向下平移两个单位再向左平移2个单位所得,
因此点N可由点M先向下平移两个单位再向左平移2个单位所得,
∴点N的坐标为(2m-2,m-2),
∵点N在抛物线y=
| 1 |
| 3 |
∴
| 1 |
| 3 |
整理得:4m2-19m+18=0,
解得:m1=
19+
| ||
| 8 |
19-
| ||
| 8 |
∴点M的坐标为(
19+
| ||
| 4 |
19+
| ||
| 8 |
19-
| ||
| 4 |
19-
| ||
| 8 |
Ⅱ.若该平行四边形为?APNM,如图4、图5.


由于点P可由点A先向右平移两个单位再向上平移2个单位所得,
因此点N可由点M先向右平移两个单位再向上平移2个单位所得,
∴点N的坐标为(2m+2,m+2),
∵点N在抛物线y=
| 1 |
| 3 |
∴
| 1 |
| 3 |
整理得:4m2-3m-10=0,
解得:m3=2,m4=-
| 5 |
| 4 |
∴点M的坐标为(4,2)或(-
| 5 |
| 2 |
| 5 |
| 4 |
综上所述:符合条件的点M的坐标为:
(
19+
| ||
| 4 |
19+
| ||
| 8 |
19-
| ||
| 4 |
19-
| ||
| 8 |
| 5 |
| 2 |
| 5 |
| 4 |
点评:本题主要考查了用待定系数法求出二次函数及一次函数的解析式、旋转的性质、解一元二次方程等知识,综合性比较强,运用割补法是解决第(1)②小题的关键,运用平移的方法得到点M与点N坐标之间的关系是解决第(2)②小题的关键.

练习册系列答案
相关题目
计算下列各题
(1)-24+19-(-16)+(-11);
(2)-32+[30-(-2)×9]÷6;
(3)-7+320÷(-4)2×(-
)+3;
(4)
÷[
-(-2+2
)]×(-8).
(1)-24+19-(-16)+(-11);
(2)-32+[30-(-2)×9]÷6;
(3)-7+320÷(-4)2×(-
| 1 |
| 2 |
(4)
| 1 |
| 12 |
| 1 |
| 4 |
| 1 |
| 3 |
在直角坐标系中y=-3x+2与x轴的交点坐标是( )
A、(
| ||
B、(-
| ||
C、(0,-
| ||
D、(0,
|