题目内容
如图，把边长为3的正三角形绕着它的中心旋转180°后，则新图形与原图形重叠部分的面积为
- A.
- B.
- C.
- D.
A
分析：根据等边三角形的特殊性，重叠部分为正六边形，四周空白部分的小三角形是等边三角形，从而得出重叠部分的面积是△ABC与三个小等边三角形的面积之差．
解答：根据旋转的意义，图中空白部分的小三角形也是等边三角形，且边长为1，面积是△ABC的
，
仔细观察图形，重叠部分的面积是△ABC与三个小等边三角形的面积之差，
△ABC的面积是
，一个小等边三角形的面积是，所以重叠部分的面积是-3×=．
故选A．
点评：本题考查旋转的性质：旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．要注意旋转的三要素：①定点-旋转中心；②旋转方向；③旋转角度．
分析：根据等边三角形的特殊性，重叠部分为正六边形，四周空白部分的小三角形是等边三角形，从而得出重叠部分的面积是△ABC与三个小等边三角形的面积之差．
解答：根据旋转的意义，图中空白部分的小三角形也是等边三角形，且边长为1，面积是△ABC的
，仔细观察图形，重叠部分的面积是△ABC与三个小等边三角形的面积之差，
△ABC的面积是
，一个小等边三角形的面积是，所以重叠部分的面积是-3×=．故选A．
点评：本题考查旋转的性质：旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．要注意旋转的三要素：①定点-旋转中心；②旋转方向；③旋转角度．
练习册系列答案
相关题目
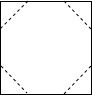如图，把边长为1m的正方形木板锯掉四个角做成正八边形的桌面，设正八边形的桌面的边长为xm，则可列出关于x的方程为（ ）| A、（1-x）2=2x2 | ||||
| B、（1-x）2=x2 | ||||
| C、（1-x）2=4x2 | ||||
D、
|
如图，把边长为1m的正方形木板锯掉四个角做成正八边形的桌面，设正八边形的桌面的边长为xm，则可列出关于x的方程为
