题目内容
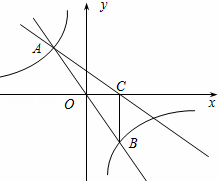
如图,在直角坐标系xOy中,直线y1=mx与双曲线y2=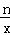 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△BOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△BOC的面积是1.
(1)求m、n的值;
(2)求直线AC的解析式;
(3)结合图象直接写出当mx>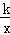 时,x的取值范围.
时,x的取值范围.
考点: 反比例函数与一次函数的交点问题.
分析: (1)由题意,根据对称性得到B的横坐标为1,确定出C的坐标,根据三角形AOC的面积求出B的纵坐标,确定出A坐标,将A坐标代入一次函数与反比例函数解析式,即可求出m与n的值;
(2)设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,即可确定出直线AC的解析式.
(2)根据A、B的坐标,然后观察函数图象求解.
解答: 解:(1)∵直线y=mx与双曲线y=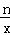 相交于A(﹣1,a)、B两点,
相交于A(﹣1,a)、B两点,
∴B(1,﹣a).
∵△BOC的面积是1,BC⊥x轴,垂足为C,
∴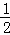 ×1×a=1,
×1×a=1,
∴a=2,
∴A(﹣1,2).
将A(﹣1,2)代入y=mx,y=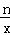 可得m=﹣2,n=﹣2;
可得m=﹣2,n=﹣2;
(2)设直线AC的解析式为y=kx+b,
∵y=kx+b经过点A(﹣1,2)、C(1,0)
∴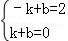 ,
,
解得k=﹣1,b=1,
∴直线AC的解析式为y=﹣x+1.
(3)由图象可知:当mx> 时,x<﹣1或0<x<1.
时,x<﹣1或0<x<1.
点评: 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:反比例函数的图象与性质,待定系数法确定函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
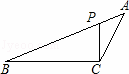
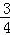 ,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).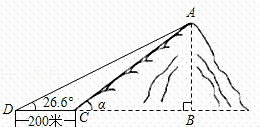
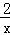 (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=
(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2,顶点P3在反比例函数y=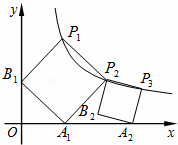
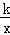 (k≠0)在第一象限内的图象经过点D、E,且D点的横坐标是它的纵坐标的2倍.
(k≠0)在第一象限内的图象经过点D、E,且D点的横坐标是它的纵坐标的2倍.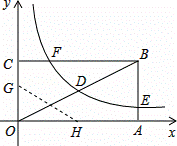
 )2+(﹣1)101﹣0.25+(
)2+(﹣1)101﹣0.25+( )2÷(﹣
)2÷(﹣ )5÷|﹣8|
)5÷|﹣8| ,AB的长为( )
,AB的长为( ) B.8 C.4
B.8 C.4 D.4
D.4