Question

在三角形ABC中，∠ABC，∠ACB的平分线相交于D，若∠BDC=125°，则∠A为

 

．

Answer 1

分析：在△BCD中根据三角形的内角和定理求得∠DBC与∠DCB的和，然后根据角平分线的定义可以证得：∠DBC+∠DCB=

1

2

（∠ABC+∠ACB），求出∠ABC+∠ACB，根据三角形的内角和定理即可求得∠A的度数．

解答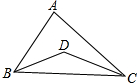：解：∵在△BCD中，∠DBC+∠DCB+∠BDC=180°
∴∠DBC+∠DCB=180°-125°=55°．
∵BD和CD是∠ABC，∠ACB的角平分线，
∴∠DBC=

1

2

∠ABC，∠DCB=

1

2

∠ACB
∴∠DBC+∠DCB=

1

2

（∠ABC+∠ACB）
∴∠ABC+∠ACB=2（∠DBC+∠DCB）=2×55=110°．
又∵△ABC中，∠ABC+∠ACB+∠A=180°，
∴∠A=180°-（∠ABC+∠ACB）=180°-110°=70°．
故答案是：70°．

点评：本题考查了三角形的内角和定理以及角平分线的定义，关键是根据角平分线的定义得到：∠DBC+∠DCB=

1

2

（∠ABC+∠ACB）．