Question

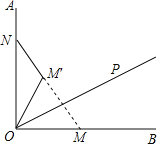
【题目】如图，∠AOB=90°，点P为∠AOB内部一点，作射线OP，点M在射线OB上，且OM=，点M′与点M关于射线OP对称，且直线MM′与射线OA交于点N．当△ONM'为等腰三角形时，ON的长为______．

Answer 1

【答案】3或1

【解析】

如图分两种情况，Ⅰ．M'在∠AOB内部，Ⅱ．M'在∠AOB外部，由已知和等腰三角形性质、利用三角函数列方程，解直角三角形即可解答．

解：M'位置有两种情况，

Ⅰ．M'在∠AOB内部，如图1，

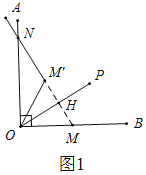
∵点M′与点M关于射线OP对称，△ONM'为等腰三角形，

∴M′N=OM′=OM=，MH=M′H，

∵∵∠AOB=90°，cos∠OMN=

∴，

解得MH=，

∴MN=2，

在Rt△MON中，ON===3

Ⅱ．M'在∠AOB外部，如图2，过N点作QN⊥OM′，

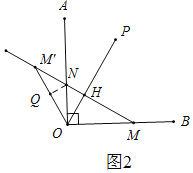
∵△ONM'为等腰三角形，即M′N=ON，

∴M′Q=M′O，

∵OM=，点M′与点M关于射线OP对称，

∴M′Q=，OM=OM′，

∴∠OM′M=∠OMM′，cos∠OM′M=，cos∠OMM′=，

设ON=M′N=x，NH=M′H=y，

，

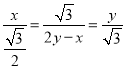解得：x=1，y=，

综上所述：当△ONM'为等腰三角形时，ON的长为3或1．

故答案为3，1．