Question

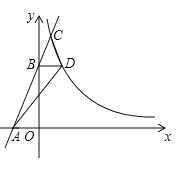
【题目】如图，在平面直角坐标系中，直线经过点，与轴交于点，与反比例函数交于点，过作轴，交反比例函数于点，连接，．

（1）求，的值；

（2）求的面积；

（3）设为直线上一点，过点作轴，交反比例函数于点，若以点，，，为顶点的四边形为平行四边形，求点的坐标．

Answer 1

【答案】（1），；（2）；（3）或

【解析】

(1) 把点代入直线得到b的值，再求解C的坐标。用待定系数法求解k的值即可得到答案；

(2) 根据一次函数的解析式得到B（0，4），把y=4代入得到，根据三角形的面积公式即可得到结论；

(3) 根据平行四边形的性质得到EF=AO=2，设点E（t，2t+4），①当点E位于点F的左侧时，得到点F（t+2，2t+4），②当点E位于点F的右侧时，得到点F（t-2，2t+4），解方程即可得到结论．

解：（1）把点代入直线得到：

，

直线

当，则，即点

即反比例函数：

（2）直线交轴于

轴，

当，则，即点

；

（3）点，，，构成平行四边形

又

设点

①当点位于点左侧时

则点

则

②当点位于点右侧时，

则点，

则，

，

，

，

，

综上所述，若以点A，O，E，F为顶点的四边形为平行四边形，点E的坐标为或；