题目内容
正多边形的边长为2,中心到边的距离为 ,则这个正多边形的边数为________.
,则这个正多边形的边数为________.
6
分析:设正多边形的中心为O点,AB为边长,OD⊥AB,垂足为D,依题意得AB=2,OD= ,由正多边形的性质可知OA=OB,根据等腰三角形的性质,可知AD=
,由正多边形的性质可知OA=OB,根据等腰三角形的性质,可知AD= AB=1,∠AOB=2∠AOD,在Rt△AOD中,解直角三角形求∠AOD,再求∠AOB,确定正多边形的边数.
AB=1,∠AOB=2∠AOD,在Rt△AOD中,解直角三角形求∠AOD,再求∠AOB,确定正多边形的边数.
解答: 解:如图,设正多边形的中心为O点,AB为边长,
解:如图,设正多边形的中心为O点,AB为边长,
过O点作OD⊥AB,垂足为D,
依题意得AB=2,OD= ,
,
∵OA=OB,
∴AD= AB=1,∠AOB=2∠AOD,
AB=1,∠AOB=2∠AOD,
在Rt△AOD中,tan∠AOD=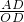 =
= =
= ,
,
∴∠AOD=30°,
∴∠AOB=2∠AOD=60°,
∴正多边形的边数= =6.
=6.
故答案为:6.
点评:本题考查了正多边形和圆.关键是画出正多边形的两条半径与一边构成的等腰三角形,作等腰三角形底边上的高,把问题转化到直角三角形中求解.
分析:设正多边形的中心为O点,AB为边长,OD⊥AB,垂足为D,依题意得AB=2,OD=
 ,由正多边形的性质可知OA=OB,根据等腰三角形的性质,可知AD=
,由正多边形的性质可知OA=OB,根据等腰三角形的性质,可知AD= AB=1,∠AOB=2∠AOD,在Rt△AOD中,解直角三角形求∠AOD,再求∠AOB,确定正多边形的边数.
AB=1,∠AOB=2∠AOD,在Rt△AOD中,解直角三角形求∠AOD,再求∠AOB,确定正多边形的边数.解答:
 解:如图,设正多边形的中心为O点,AB为边长,
解:如图,设正多边形的中心为O点,AB为边长,过O点作OD⊥AB,垂足为D,
依题意得AB=2,OD=
 ,
,∵OA=OB,
∴AD=
 AB=1,∠AOB=2∠AOD,
AB=1,∠AOB=2∠AOD,在Rt△AOD中,tan∠AOD=
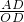 =
= =
= ,
,∴∠AOD=30°,
∴∠AOB=2∠AOD=60°,
∴正多边形的边数=
 =6.
=6.故答案为:6.
点评:本题考查了正多边形和圆.关键是画出正多边形的两条半径与一边构成的等腰三角形,作等腰三角形底边上的高,把问题转化到直角三角形中求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
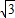 ,则这个正多边形的边数为 .
,则这个正多边形的边数为 . ,则这个正多边形的边数为 .
,则这个正多边形的边数为 .