题目内容
10.-$\frac{1}{8}$的立方根是-$\frac{1}{2}$,函数y=$\frac{\sqrt{x+2}}{x-3}$中自变量x的取值范围是x≥-2且x≠3.分析 根据立方根的定义可求-$\frac{1}{8}$的立方根;根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围.
解答 解:∵(-$\frac{1}{2}$)3=-$\frac{1}{8}$,
∴-$\frac{1}{8}$的立方根是-$\frac{1}{2}$;
根据题意得:x+2≥0且x-3≠0,
解得:x≥-2且x≠3.
故答案为-$\frac{1}{2}$;x≥-2且x≠3.
点评 本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
同时考查了立方根的定义.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
1. 如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )
如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )
 如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )
如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )| A. | $\frac{4}{3}$ | B. | 3 | C. | 5 | D. | $\frac{27}{4}$ |
15.点A(-3,2)关于原点对称的点为点B,则点B的坐标是( )
| A. | (3,2) | B. | (-3,2) | C. | (3,-2) | D. | (-2,3) |
19. 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )| A. | 4.8m | B. | 6.4m | C. | 8m | D. | 10m |
20.下列计算正确的是( )
| A. | (-$\frac{3}{2}$)-1=$\frac{3}{2}$ | B. | $\frac{1}{a}+\frac{1}{b}=\frac{2}{a+b}$ | C. | $\frac{{a}^{2}-{b}^{2}}{a-b}=a+b$ | D. | (-$\frac{1}{20}$)0=0 |
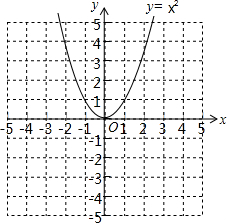 二次函数y=x2的图象如图,请将此图象向右平移1个单位,再向下平移4个单位.
二次函数y=x2的图象如图,请将此图象向右平移1个单位,再向下平移4个单位.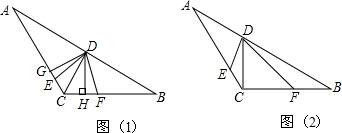
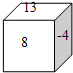 如图,正方体的每个面上都写有一个实数,已知相对的两个面上的两数之和相等,若13、8、-4的对面的数分别是x、y、z,则2x-3y+z的值为( )
如图,正方体的每个面上都写有一个实数,已知相对的两个面上的两数之和相等,若13、8、-4的对面的数分别是x、y、z,则2x-3y+z的值为( )