题目内容
某小区欲建两栋新楼房,它们的高AB=CD=20米,两楼间距设计为30米.现需了 解甲楼对乙楼的采光的影响情况,冬日正午太阳光与水平线的夹角为30°时,
解甲楼对乙楼的采光的影响情况,冬日正午太阳光与水平线的夹角为30°时,(1)求甲楼的影子在乙楼上有多高?
(2)若乙楼1楼住户的窗台距地面1米,为不影响乙楼的采光,两楼间距应至少为多少米?(精确到0.1米.
| 3 |
| 2 |
分析: (1)如图设光线与CD交于E,过E作EF⊥AB于F,则四边形FBDE为矩形,
(1)如图设光线与CD交于E,过E作EF⊥AB于F,则四边形FBDE为矩形,
∴EF=BD=30,∵∠AEF=30°∴AF=EF•tan30°,由此可以求出AF,然后求出ED;
(2)当ED=BF=1时,AF=19,此时,BD=EF=
,由此可以求出DB,即两楼间距.
 (1)如图设光线与CD交于E,过E作EF⊥AB于F,则四边形FBDE为矩形,
(1)如图设光线与CD交于E,过E作EF⊥AB于F,则四边形FBDE为矩形,∴EF=BD=30,∵∠AEF=30°∴AF=EF•tan30°,由此可以求出AF,然后求出ED;
(2)当ED=BF=1时,AF=19,此时,BD=EF=
| AF |
| tan30° |
解答:解:(1)如图,设光线与CD交于E,过E作EF⊥AB 于F,
于F,
则四边形FBDE为矩形,
∴EF=BD=30,
∵∠AEF=30°,
∴AF=EF•tan30°≈17.3,
∴ED=BF=AB-AF=20-17.3=2.7,BF≈34.6米,
ED≈2.7米;
(2)当ED=BF=1时,
AF=19,
此时,BD=EF=
=
≈32.9,
∴间距约为32.9米.
 于F,
于F,则四边形FBDE为矩形,
∴EF=BD=30,
∵∠AEF=30°,
∴AF=EF•tan30°≈17.3,
∴ED=BF=AB-AF=20-17.3=2.7,BF≈34.6米,
ED≈2.7米;
(2)当ED=BF=1时,
AF=19,
此时,BD=EF=
| AF |
| tan30° |
| 19 |
| tan30° |
∴间距约为32.9米.
点评:解此题的关键是把实际问题转化为数学问题,只要把实际问题抽象到解直角三角形中,利用三角函数即可解答.

练习册系列答案
相关题目
 解甲楼对乙楼的采光的影响情况,冬日正午太阳光与水平线的夹角为30°时,
解甲楼对乙楼的采光的影响情况,冬日正午太阳光与水平线的夹角为30°时, 1.73,
1.73,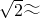 1.41)
1.41) 1.73,
1.73, 1.41)
1.41)

 1.73,
1.73, 1.41)
1.41) 1.73,
1.73, 1.41)
1.41)