��Ŀ����
��ͼ1��ƽ��֮������ϵ�У�����ֱ�������ε�ֱ�DZ�BC��x���������ϻ�������C������Ϊ��t��0����ֱ�DZ�AC=4������O��C������������ ��aΪ������a��0��������������б��AB���ڵ�E��ֱ��OA��y2=kx��kΪ������k��0��
��aΪ������a��0��������������б��AB���ڵ�E��ֱ��OA��y2=kx��kΪ������k��0��
��1����գ��ú�t�Ĵ���ʽ��ʾ��A�����꼰k��ֵ��A�� ����k=�� ����
��2���������ǰ�Ļ�������a= ʱ��
ʱ��
��������֤�������� �Ķ����ں���
�Ķ����ں��� ��ͼ���ϣ�
��ͼ���ϣ�
�ڵ����ǰ廬����EΪAB���е�ʱ����t��ֵ��
��3��ֱ��OA�������ߵ���һ������Ϊ��D����t��x��t+4��|y2��y1|��ֵ��x���������С����x��t+4ʱ��|y2��y1|��ֵ��x�������������a��t�Ĺ�ϵʽ��t��ȡֵ��Χ��
�⣺��1���ߵ�C������Ϊ��t��0����ֱ�DZ�AC=4�����A�������ǣ�t��4����
��ֱ��OA��y2=kx��kΪ������k��0������4=kt���� ��k��0����
��k��0����
��2���ٵ�a= ʱ��
ʱ�� ���䶥������Ϊ
���䶥������Ϊ ��
��
���� ����x=
����x= ʱ��
ʱ��
��� ��������
�������� �ϡ�
�ϡ�
�൱a= ʱ��������
ʱ�������� �Ķ����ں���
�Ķ����ں��� ��ͼ���ϡ�
��ͼ���ϡ�
����ͼ1������E��EK��x���ڵ�K��
��AC��x�ᣬ��AC��EK��
�ߵ�E���߶�AB���е㣬��KΪBC���е㡣
��EK�ǡ�ACB����λ�ߡ�
��EK= AC=2��CK=
AC=2��CK= BC=2����E��t+2��2����
BC=2����E��t+2��2����
�ߵ�E�������� �ϣ�
�ϣ�
�� �����t=2��
�����t=2��
�൱���ǰ廬����EΪAB���е�ʱ��t=2��
��3����ͼ2���� ��
�� ��
��
��� ����x=0���������⣬��ȥ����
����x=0���������⣬��ȥ����
���D������� ��
��
�� ʱ��|y2��y1|=0���������
ʱ��|y2��y1|=0��������� ����
���� ��
��
�� ��
��
�൱ ʱ��
ʱ�� ȡ�����ֵ��
ȡ�����ֵ��
�ֵ� ʱ��
ʱ�� ȡ����Сֵ0��
ȡ����Сֵ0��
�൱ ʱ��
ʱ�� ��ֵ��x���������С����
��ֵ��x���������С���� ʱ��
ʱ�� ��ֵ��x�����������
��ֵ��x�����������
�����⣬�� ����
���� �����
����� �����
����� ��
��
����������a��t�Ĺ�ϵʽΪ ��t��ȡֵ��ΧΪ
��t��ȡֵ��ΧΪ ��
��
���������������1�����������õ�A�ĺ��������C����ͬ����A�������꼴���߶�AC�ij��ȣ��ѵ�A���������ֱ��OA�Ľ���ʽ����k��ֵ��
��2�������������y1�Ķ������꣬Ȼ��Ѹ�������뺯�� �����õ����㺯������ʽ
�����õ����㺯������ʽ ������ʾ�ö����ں���
������ʾ�ö����ں��� ͼ���ϣ���֮���ö��㲻�ں���
ͼ���ϣ���֮���ö��㲻�ں��� ͼ���ϡ�
ͼ���ϡ�
����ͼ1������E��EK��x���ڵ�K����EK�ǡ�ACB����λ�ߣ����Ը�����������λ�߶��������E�����꣬�ѵ�E��������������� �������t=2��
�������t=2��
��3����ͼ2��������������ֱ���ཻ������õ�D�������� ����
���� ���ɴ˿������a��t�Ĺ�ϵʽ����
���ɴ˿������a��t�Ĺ�ϵʽ���� ���
��� ȡ�����ֵʱ��xֵ
ȡ�����ֵʱ��xֵ ��ͬʱ��
��ͬʱ�� ʱ��
ʱ�� ȡ����Сֵ0���ó���
ȡ����Сֵ0���ó��� ʱ��
ʱ�� ��ֵ��x���������С����
��ֵ��x���������С���� ʱ��
ʱ�� ��ֵ��x����������Ӷ������⣬��
��ֵ��x����������Ӷ������⣬�� �����
����� �����t��ȡֵ��Χ��
�����t��ȡֵ��Χ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�һ��������˾ӵ��ij���ͺŵ�����100������˾�ھ�Ӫ�з���ÿ�����������x(Ԫ)��ÿ������ij�����(y)�����¹�ϵ��
| x | 3000 | 3200 | 3500 | 4000 |
| y | 100 | 96 | 90 | 80 |
��2����֪����ij�ÿ��ÿ����Ҫά����150Ԫ��δ����ij�ÿ��ÿ����Ҫά����50Ԫ���ú�x��x��3000���Ĵ���ʽ���:
| ����ij����� | | ���ij����� | |
| ���ÿ������������ | | ����δ����ij���ÿ�µ�ά���� | |
��2013���㽭����10�֣�Ϊӭ���й�ɭ���ᣬij�̼Ҽƻ��ӳ��Ҳɹ�A��B���ֲ�Ʒ��20������Ʒ�IJɹ����ۣ�Ԫ/�����Dzɹ�������������һ�κ������±��ṩ�˲��ֲɹ����ݣ�
| �ɹ����������� | 1 | 2 | �� |
| A��Ʒ���ۣ�Ԫ/���� | 1480 | 1460 | �� |
| B��Ʒ���ۣ�Ԫ/���� | 1290 | 1280 | �� |
��2�����̼��볧��Э�̣��ɹ�A��Ʒ������������B��Ʒ������
 ����A��Ʒ�ɹ����۲�����1200Ԫ������̼ҹ��м��ֽ���������
����A��Ʒ�ɹ����۲�����1200Ԫ������̼ҹ��м��ֽ�����������3�����̼ҷֱ���1760Ԫ/����1700Ԫ/�������۵����۳�A��B���ֲ�Ʒ����ȫ�����꣮�ڣ�2���������£���ɹ�A�ֲ�Ʒ���ټ�ʱ������������������

 A����ô���ı���ʽ�ɱ�ʾΪ��
A����ô���ı���ʽ�ɱ�ʾΪ�� ]
]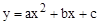 ����A��B��C���㣬����ΪF��
����A��B��C���㣬����ΪF��

 ��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪A�������ΪA����2��0����
��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪A�������ΪA����2��0����
