题目内容
在平面直角坐标系中,一个二次函数的图象经过点A(1,0)、B(3,0)两点.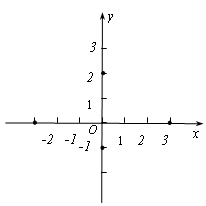
(1)写出这个二次函数的对称轴;
(2)设这个二次函数的顶点为D,与y轴交于点C,它的对称轴与x轴交于点E,连接AD、DE和DB,当△AOC与△DEB相似时,求这个二次函数的表达式。
[提示:如果一个二次函数的图象与x轴的交点为 A,那么它的表达式可表示为:
A,那么它的表达式可表示为: ]
]
解:(1)对称轴为直线:x=2。
(2)∵A(1,0)、B(3,0),∴设这个二次函数的表达式 。
。
当x=0时,y=3a,当x=2时,y= 。
。
∴C(0,3a),D(2,-a),∴OC=|3a|。
∵A(1,0)、E(2,0),∴OA=1,EB=1,DE=}-a|=|a|。
在△AOC与△DEB中,
∵∠AOC=∠DEB=90°,∴当 时,△AOC∽△DEB。
时,△AOC∽△DEB。
∴ 时,解得
时,解得 或
或 。
。
当 时,△AOC∽△BED,
时,△AOC∽△BED,
∴ 时,此方程无解。
时,此方程无解。
综上所述,所求二次函数的表达式为: 或
或 ,即
,即 或
或 。
。
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某公司销售一种进价为20元/个的计算机,其销售量y(万个)与销售价格x(元/个)的变化如下表:
| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万个)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
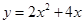 .
. 的形式(要求写出配方过程);
的形式(要求写出配方过程); 与直线y=x交于点A,点B在直线
与直线y=x交于点A,点B在直线 过点A,O,B,顶点为点E.
过点A,O,B,顶点为点E.

 ,同理
,同理 ,所以AB的中点坐标为
,所以AB的中点坐标为 .由勾股定理得
.由勾股定理得 ,所以A、B两点间的距离公式为
,所以A、B两点间的距离公式为 .
.
 (a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
 时:
时: 的图象上;
的图象上; 与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
