题目内容
已知0≤a-b≤1,且1≤a+b≤4,则a的取值范围是 .
考点:不等式的性质
专题:
分析:根据不等式的性质,先将两不等式相加,得到1≤2a≤5,再两边同时除以2,即可求出a的取值范围.
解答:解:∵0≤a-b≤1,且1≤a+b≤4,
∴0+1≤a-b+a+b≤1+4,即1≤2a≤5,
∴
≤a≤
.
故答案为
≤a≤
.
∴0+1≤a-b+a+b≤1+4,即1≤2a≤5,
∴
| 1 |
| 2 |
| 5 |
| 2 |
故答案为
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查了不等式的基本性质:
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.
(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.
(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.
(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列各对数中,互为相反数的是( )
| A、-|-2|和+(-2) |
| B、+(-6)和-(+6) |
| C、(-4)3和-43 |
| D、(-5)4和-54 |
 已知AB、AC是⊙O的切线,B、C是切点,BD是⊙O的直径,连接AO、CD.
已知AB、AC是⊙O的切线,B、C是切点,BD是⊙O的直径,连接AO、CD. 如图,正方形ABCD的边长为8,点M在边DC上,且DM=2,M、N两点关于对角线AC对称,则tan∠ADN=
如图,正方形ABCD的边长为8,点M在边DC上,且DM=2,M、N两点关于对角线AC对称,则tan∠ADN= 如图,已知∠1=∠2,∠B=∠C,AF=AE,求证:CD=BD.
如图,已知∠1=∠2,∠B=∠C,AF=AE,求证:CD=BD.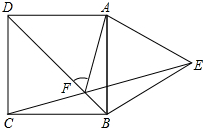 如图,四边形ABCD为正方形,以AB为边向正方形外作等边三角形ABE,CE与DB相交于点F,则
如图,四边形ABCD为正方形,以AB为边向正方形外作等边三角形ABE,CE与DB相交于点F,则