题目内容
 如图(1),“
如图(1),“ ”形是由边长为a的大正方形在右下角剪去一个边长为b(b<a)的小正方形得到的,沿虚线将它剪成“Ⅰ”和“Ⅱ”两部分,并将Ⅱ移到图(2)的位置构成一个长方形.
”形是由边长为a的大正方形在右下角剪去一个边长为b(b<a)的小正方形得到的,沿虚线将它剪成“Ⅰ”和“Ⅱ”两部分,并将Ⅱ移到图(2)的位置构成一个长方形.
(1)分别写出图1、图2中阴影部分的面积.
(2)由结果你得到什么公式?
解:(1)图1中阴影部分的面积:a2-b2;
图2中阴影部分的面积:(a+b)(a-b);
(2)a2-b2=(a+b)(a-b).
分析:(1)利用正方形的面积差求出图1的面积,图2的长为(a+b),宽为(a-b),由长方形的面积求出答案即可;
(2)两个阴影部分面积相等,由(1)中的式子联立等式即可.
点评:此题考查利用正方形和长方形面积计算方法推导平方差公式.
图2中阴影部分的面积:(a+b)(a-b);
(2)a2-b2=(a+b)(a-b).
分析:(1)利用正方形的面积差求出图1的面积,图2的长为(a+b),宽为(a-b),由长方形的面积求出答案即可;
(2)两个阴影部分面积相等,由(1)中的式子联立等式即可.
点评:此题考查利用正方形和长方形面积计算方法推导平方差公式.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目

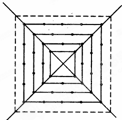
 7、用八根木条钉成如图所示的八边形木架,要使它不变形,至少要钉上木条的根数是( )
7、用八根木条钉成如图所示的八边形木架,要使它不变形,至少要钉上木条的根数是( )
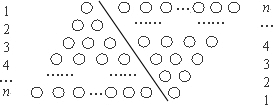
 如图所示,有一个形如四边形的点阵,第1层每边有两个点,第2层每边有三个点,第3层每边有四个点,依此类推.
如图所示,有一个形如四边形的点阵,第1层每边有两个点,第2层每边有三个点,第3层每边有四个点,依此类推.