题目内容
已知△ABC.
(1)若∠BAC=40°,画∠BAC和外角∠ACD的角平分线相交于O1点(如图①),求∠BO1C的度数;
(2)在(1)的条件下,再画∠O1BC和∠O1CD的角平分线相交于O2点(如图②),求∠BO2C的度数;
(3)若∠BAC=n°,按上述规律继续画下去,请直接写出∠BO2012C的度数.

(1)若∠BAC=40°,画∠BAC和外角∠ACD的角平分线相交于O1点(如图①),求∠BO1C的度数;
(2)在(1)的条件下,再画∠O1BC和∠O1CD的角平分线相交于O2点(如图②),求∠BO2C的度数;
(3)若∠BAC=n°,按上述规律继续画下去,请直接写出∠BO2012C的度数.

分析:由∠O1CD=∠O1+∠O1BC,∠ACD=∠ABC+∠A,而O1B、O1C分别平分∠ABC和∠ACD,得到∠ACD=2∠O1CD,∠ABC=2∠O1BC,于是有∠A=2∠O1,同理可得∠O1=2∠O2,即∠A=22∠O2,因此找出规律.
解答:解:∵O1B、O1C分别平分∠ABC和∠ACD,
∴∠ACD=2∠O1CD,∠ABC=2∠O1BC,
而∠O1CD=∠O1+∠O1BC,∠ACD=∠ABC+∠A,
∴∠A=2∠01=40°,
∴∠O1=20°,
同理可得∠O1=2∠O2,
即∠A=22∠02=40°,
∴∠O2=10°,
∴∠A=2n∠An,
∴∠An=n°×(
)n.
则∠BO2012C=(
)2012•n0.
∴∠ACD=2∠O1CD,∠ABC=2∠O1BC,
而∠O1CD=∠O1+∠O1BC,∠ACD=∠ABC+∠A,
∴∠A=2∠01=40°,
∴∠O1=20°,
同理可得∠O1=2∠O2,
即∠A=22∠02=40°,
∴∠O2=10°,
∴∠A=2n∠An,
∴∠An=n°×(
| 1 |
| 2 |
则∠BO2012C=(
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形的外角性质以及角平分线性质,难度适中.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知ABC的三边满足a2+b2+c2-ab-bc-ac=0,则这个三角形的形状是( )
| A、直角三角形 | B、等腰三角形 | C、等腰直角三角形 | D、等边三角形 |
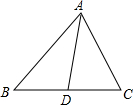 如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )
如图,已知ABC中,AD为BC边上的中线,且AB=4cm,AC=3cm,则AD的取值范围是( )| A、3<AD<4 | ||||
| B、1<AD<7 | ||||
C、
| ||||
D、
|
已知△ABC中,cosA=
,tgB=1,则△ABC的形状是( )
| 1 |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
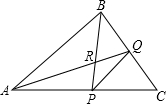 如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于
如图,已知△ABC,∠B的平分线交边AC于P,∠A的平分线交边BC于Q,如果过点P、Q、C的圆也过△ABC的内心R,且PQ=1,则PR的长等于