题目内容

分解因式：x2-3x（x-3）-9=
 
．
考点：因式分解-十字相乘法等
专题：
分析：利用ax2+bx+c（a≠0）型的式子的因式分解这种方法的关键是把二次项系数a分解成两个因数a1，a2的积a1•a2，把常数项c分解成两个因数c1，c2的积c1•c2，并使a1c2+a2c1正好是一次项b，那么可以直接写成结果：ax2+bx+c=（a1x+c1）（a2x+c2），进而求出即可．
解答：解：x2-3x（x-3）-9
=x2-3x2+9x-9
=-2x2+9x-9
=（x-3）（-2x+3）．
故答案为：（x-3）（-2x+3）．
点评：此题主要考查了十字相乘法分解因式，正确分解常数项以及二次项系数是解题关键．
练习册系列答案
相关题目
化简：（
2
a-1
-
1
a+1
）×（a2-1）=
 
．
如图，CD∥AB，OE平分∠AOD，OF⊥OE，OG⊥CD，∠D=50°，则下列结论：①∠AOE=65°，②OF平分∠BOD；③∠GOE=∠DOF；④∠AOE=2∠GOD，其中正确结论的个数是（　　）
A、1B、2C、3D、4
如图①，分别以Rt△ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．
（1）如图②，分别以Rt△ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，写出它们的关系；（不必证明）
（2）如图③，分别以Rt△ABC三边为边向外作正三角形，其面积分别用S1，S2，S3表示，确定它们的关系并证明；
（3）若分别以Rt△ABC三边为边向外作三个正多边形，其面积分别用S1，S2，S3表示，请你猜想S1，S2，S3之间的关系．
如图，在矩形ABCD中，AB=9，BC=12，点E是BC的中点，点F是CD边上的任意一点，当△AEF的周长最小时，DF=
 
．
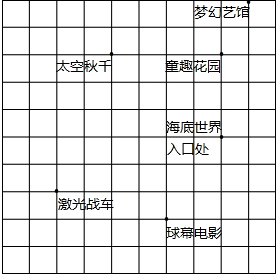如图是“欢欢游乐城”的平面示意图，如果用（8，5）表示入口处的位置，那么（8，8）表示的位置是（　　）
A、太空秋千B、梦幻艺馆
C、童趣花园D、球幕电影
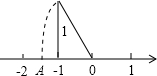如图，数轴上的点A所表示的数为（　　）
A、
2
B、-
2
C、
2
-1
D、1-
2
若A（-4，yl），B（-3，y2），C（l，y3）为二次函数y=ax2+6ax-5（a＞0）的图象上的三点，则yl，y2，y3的大小关系是
 
．（用“＜”号连接）
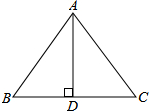如图，在等腰△ABC中，AD是底边BC上的高，AB=AC=5，BC=6，P是线段AD上一个动点，记AP长为x，当A在以P为圆心，PB为半径的圆的外部时，求x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网