题目内容
如图,一次函数y=-12 x+4的图象交x轴于点A,交正比例函数y=![]() x的图象于点B.矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴上方,DC=2,DE=4.当点C坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
x的图象于点B.矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴上方,DC=2,DE=4.当点C坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
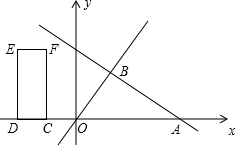
(1)求点B的坐标.
(2)矩形CDEF运动t秒时,直接写出C、D两点的坐标.
(3)当点B在矩形CDEF的一边上时,求t的值.
(4)设CF、DE分别交折线OBA于M、N两点,当四边形MCDN为直角梯形时,求t的取范围.
(1)点B的坐标为(2,3)
(2)C、D两点的坐标为:(-2+2t,0)(-4+2t,0)
(3)t=3 (4)t的取值范围是:2<t<5.
解析:解:(1)由 y=![]() x y=-
x y=-![]() x+4 ,
x+4 ,
解得: x=2 y=3 .
∴点B的坐标为(2,3).
(2)∵矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
∴C、D两点的坐标为:(-2+2t,0)(-4+2t,0).
(3)当B点在CF上时,则
-2+2t=2,
t=2.
当B在ED上时,则
-4+2t=2,
t=3.
(4)根据题意得,当D点在点O处时,t=2,
当点C在A处时,t=5,
又∵当DC在OA之间运动时,
四边形MCDN为直角梯形.
∴t的取值范围是:2<t<5.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数