题目内容
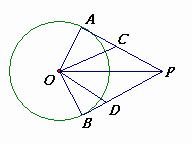
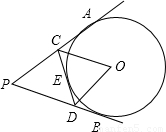
 如图PA、PB、CD分别切⊙O于A、B、E,∠APB=54°,则∠COD=
如图PA、PB、CD分别切⊙O于A、B、E,∠APB=54°,则∠COD=
- A.36°
- B.63°
- C.126°
- D.46°
B
分析:连接OA,OB,OE,根据切线长定理,得∠AOC=∠COE,∠BOD=∠DOE,从而得∠COD= ∠AOB,再由∠APB=54°,求得∠COD.
∠AOB,再由∠APB=54°,求得∠COD.
解答: 解:如图,连接OA,OB,OE,
解:如图,连接OA,OB,OE,
∵PA、PB、CD分别切⊙O于A、B、E,
∴∠AOC=∠EOC,
同理∠BOD=∠DOE,
∴∠COD=∠COE+∠DOE= ∠AOB,
∠AOB,
∵∠APB=54°,
∴∠AOB=126°,
∴∠COD=63°.
故选B.
点评:本题考查了切线长定理和三角形的内角和定理,是基础知识要熟练掌握.
分析:连接OA,OB,OE,根据切线长定理,得∠AOC=∠COE,∠BOD=∠DOE,从而得∠COD=
 ∠AOB,再由∠APB=54°,求得∠COD.
∠AOB,再由∠APB=54°,求得∠COD.解答:
 解:如图,连接OA,OB,OE,
解:如图,连接OA,OB,OE,∵PA、PB、CD分别切⊙O于A、B、E,
∴∠AOC=∠EOC,
同理∠BOD=∠DOE,
∴∠COD=∠COE+∠DOE=
 ∠AOB,
∠AOB,∵∠APB=54°,
∴∠AOB=126°,
∴∠COD=63°.
故选B.
点评:本题考查了切线长定理和三角形的内角和定理,是基础知识要熟练掌握.

练习册系列答案
相关题目
 如图PA、PB、CD分别切⊙O于A、B、E,∠APB=54°,则∠COD=( )
如图PA、PB、CD分别切⊙O于A、B、E,∠APB=54°,则∠COD=( )| A、36° | B、63° | C、126° | D、46° |