Question

如图，抛物线的对称轴为轴，且经过（0,0），（）两点，点P在抛物线上运动，以P为圆心的⊙P经过定点A（0,2），

(1)求的值；    （收集整理cjzl）

(2)求证：点P在运动过程中，⊙P始终与轴相交；

（3）设⊙P与轴相交于M，N 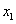（＜）两点，当△AMN为等腰三角形时，求圆心P的纵坐标。

Answer 1

（1）

   （2）设P(x,y), ⊙P的半径r=，又，则r=，化简得：r=＞，∴点P在运动过程中，⊙P始终与轴相交；

  （3）设P()，∵PA=，作PH⊥MN于H,则PM=PN=,又PH=,则MH=NH=，故MN=4，∴M(，0)，N(,0)，

   又A(0，2)，∴AM=,AN=

当AM=AN时，解得=0，

当AM=MN时, =4，解得：=，则=；

当AN=MN时, =4，解得：= ，则=

综上所述，P的纵坐标为0或或；