题目内容
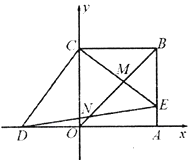
【题目】如图，在平面直角坐标系中，正方形
两顶点为
，
，点D的坐标为
，在
上取点E，使得
，连接
，分别交
，
于M，N两点．
（1）求证：
；
（2）求点E的坐标和线段
所在直线的解析式；
（3）在M，N两点中任选一点求出它的坐标．
【答案】（1）详见解析；（2）点E的坐标是
，
；（3）点M的坐标为
，或点N的坐标为
.
【解析】
（1）由已知条件可得
，有根据
，
，即可得证；
（2）由（1）中结论，可得
，进而得出AE，得出点E坐标，设直线
的解析式为
，将点B坐标代入，即可得解；
（3）①设直线
的解析式为
，将点
，点
代入，即可得出直线解析式，联立直线CE和直线OB，即可得出点M的坐标；②设直线DE的解析式为，将点D 
，点代入即可得出解析式，联立直线DE和直线OB，即可得出点N坐标..
（1）∵正方形
中
，坐标系中
∴
又∵，正方形中
∴
（2）∵
，
∴
∴
又∵
，
∴点E的坐标是
设直线的解析式为
将点
的对应值
，
代入求得
∴所求解析式为
（3）①求点M的坐标：
设直线的解析式为
由点，点得
解得
∴直线的解析式为
解方程组
得
∴直线与直线的交点M的坐标为
②仿①的方法求得点N的坐标为
设直线DE的解析式为
由点D ，点，得
解得
∴直线DE的解析式为
联立方程组，得
解得
直线DE与直线OB的交点为N的坐标
.
阅读快车系列答案【题目】某玩具厂计划一周生产某种玩具700件，平均每天生产100件，但由于种种原因，实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产记为正、减产记为负）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +5 | －2 | －4 | +13 | －6 | +6 | －3 |
（1）根据记录的数据可知该厂星期四生产玩具 件；
（2）产量最多的一天比产量最少的一天多生产玩具 件；
（3）根据记录的数据可知该厂本周实际生产玩具 件；
（4）该厂实行每周计件工资制，每生产一件玩具可得20元，若超额完成任务，则超过部分每件另奖5元；少生产一件扣4元，那么该厂工人这一周的工资总额是多少元？
