Question

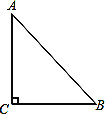
【题目】如果三角形有一边上的中线恰好等于这边的长，那么称这个三角形为“有趣三角形”，这条中线称为“有趣中线”。如图，在三角形ABC中，∠C=90°，较短的一条直角边BC=1，且三角形ABC是“有趣三角形”，求三角形ABC的“有趣中线”的长。

Answer 1

【答案】．

【解析】

试题分析：“有趣中线”分三种情况，两个直角边跟斜边，而直角三角形的斜边的中点到三顶点距离相等，不符合；两个直角边，有一种情况有趣中线为1．但是不符合较短的一条直角边边长为1，只能为另一条直角边上的中线，利用勾股定理求出即可．

试题解析：“有趣中线”有三种情况：

若“有趣中线”为斜边AB上的中线，直角三角形的斜边的中点到三顶点距离相等，不合题意；

若“有趣中线”为BC边上的中线，根据斜边大于直角边，矛盾，不成立；

若“有趣中线”为另一直角边AC上的中线，如图所示，BC=1，

设BD=2x，则CD=x，

在Rt△CBD中，根据勾股定理得：BD2=BC2+CD2，即（2x）2=12+x2，

解得：x=，

则△ABC的“有趣中线”的长等于．