题目内容
【题目】(1)尺规作图:如图,![]() 、
、![]() 是平面上两个定点,在平面上找一点
是平面上两个定点,在平面上找一点![]() ,使
,使![]() 构成等腰直角三角形,且
构成等腰直角三角形,且![]() 为直角顶点.(画出一个点
为直角顶点.(画出一个点![]() 即可)
即可)

(2)在(1)的条件下,若![]() ,
,![]() ,则点
,则点![]() 的坐标是________.
的坐标是________.
【答案】(1)见解析(2)![]()
【解析】
(1)如图作线段AB的垂直平分线MN交AB于点O,以O为圆心,OA为半径作⊙O交直线MN于C,C′,连接AC,BC,AC′BC′,点C或C′即为所求;
(2)如图,由勾股定理求出AB的长,再证明△NAE∽△BAO,求出AN,EN的长,再证明△NCD∽△NBE,求出CD,OD的长,进行可求点C的坐标,同理可求点![]() 的坐标.
的坐标.
(1)如图作线段AB的垂直平分线MN交AB于点O,以O为圆心,OA为半径作⊙O交直线MN于C,C′,连接AC,BC,AC′BC′,点C或C′即为所求.

(2)建立平面直角坐标系如图,CD⊥AN,EG⊥OB,![]() ,EG⊥OB,垂足分别为D,F,G.
,EG⊥OB,垂足分别为D,F,G.
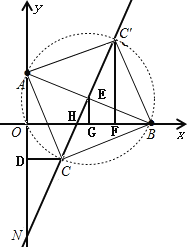
∵A(0,2),B(4,0),
∴OA=2,OB=4,
∴AB=![]()
∵E是圆心,AB是直径,
∴AE=![]() AB=
AB=![]() ,CE=
,CE=![]()
在△AOB和△AEN中,
∵∠NAE=∠BAO,∠AEN=∠AOB,
∴△AOB∽△AEN
∴![]()
∴NE=![]() ,CN=
,CN=![]() ,
,
∴AN=![]()
同理可证,△NCD∽△NAE,
∴![]() ,
,
∴![]() ,
,
∴CD=1,ND=2,
∴OD=5-2-2=1,
∴点C的坐标为(1,-1);
∵AO=2,
∴EG=1,
易证△EGH∽△NOH,
∴![]() ,即
,即![]()
∴![]() ,
,
∴HG=![]() ,OH=
,OH=![]()
∵ ![]() ,EG⊥OB,
,EG⊥OB,
∴△EHG∽△![]() ,
,
∴![]() ,即
,即 ,
,
∴![]() ,
,![]()
∴GF=1,
∴OF=2+1=3,
∴点![]() 的坐标为(3,3).
的坐标为(3,3).

练习册系列答案
相关题目