题目内容
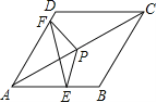
【题目】如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，以BC为直径的⊙O与AD相切，点E为AD的中点，下列结论正确的个数是（ ）
（1）AB+CD=AD；（2）S△BCE=S△ABE+S△DCE；（3）ABCD=
；（4）∠ABE=∠DCE．
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
设AD和半圆O相切的切点为F，连接OF，根据切线长定理以及相似三角形的判定和性质逐项分析即可．
设AD和半圆O相切的切点为F，
∵在直角梯形ABCD中AB∥CD，AB⊥BC，
∴
∵AB为直径，
∴AB，CD是圆的切线，
∵AD与以AB为直径的⊙O相切，
∴AB=AF，CD=DF，
∴AD=AF+DF=AB+CD，故①正确；
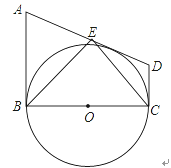
如图1，连接OE，
∵AE=DE，BO=CO，
∴OE∥AB∥CD,OE=
(AB+CD)，
∴OE⊥BC，
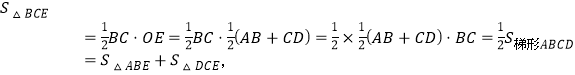故②正确；
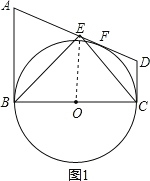
如图2，连接AO，OD，
∵AB∥CD,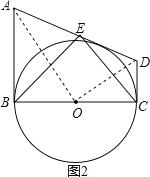
∴
∵AB，CD，AD是O的切线，
∴
∴
∴
∴∠BAO=∠DOC，
∴△ABO∽△OCD，
∴
∴
，故③正确，
如图1，∵OB=OC，OE⊥BC，
∴BE=CE，
∴∠BEO=∠CEO，
∵AB∥OE∥CD，
∴∠ABE=∠BEO，∠DCE=∠OEC，
∴∠ABE=∠DCE，故④正确，
综上可知正确的个数有4个，
故选:D.
练习册系列答案
阅读快车系列答案
相关题目
