题目内容
已知在平面直角坐标系 中,二次函数
中,二次函数 的图像经过点
的图像经过点 和点
和点 ;
;

(1)求这个二次函数的解析式;
(2)将这个二次函数的图像向上平移,交 轴于点
轴于点 ,其纵坐标为
,其纵坐标为 ,请用
,请用 的代数式表示平移后函数图象顶点
的代数式表示平移后函数图象顶点 的坐标;
的坐标;
(3)在第(2)小题的条件下,如果点 的坐标为
的坐标为 ,
, 平分
平分 ,求
,求 的值;
的值;
(1) ; (2)
; (2) ; (3)
; (3) ;
;
【解析】
试题分析:(1)把点 和点
和点 ,代入
,代入 然后解方程中即可函数解析式;
然后解方程中即可函数解析式;
(2)将函数解析式化为顶点式,可得顶点坐标,根据图象的平移规律,可得M点的坐标;
(3)根据角平分线的性质,可得全等三角形,根据全等三角形的性质,可得方程组,根据解方程组,可得答案.
试题解析:(1)由二次函数y=ax2+bx的图象经过点(1,-3)和点(-1,5),得 ,解得
,解得 ,
,
所以二次函数的解析式y=x2-4x;
(2)因为 ,所以函数顶点M坐标(2,-4),这个二次函数的图象向上平移,交y轴于点C,其纵坐标为m,顶点M坐标向上平移m,即M(2,m-4);
,所以函数顶点M坐标(2,-4),这个二次函数的图象向上平移,交y轴于点C,其纵坐标为m,顶点M坐标向上平移m,即M(2,m-4);
(3)由待定系数法,得CP的解析式为 ,如图:
,如图:

作MG⊥PC于G,设G(a, a+m),由角平分线上的点到角两边的距离相等,DM=MG.在Rt△DCM和Rt△GCM中
a+m),由角平分线上的点到角两边的距离相等,DM=MG.在Rt△DCM和Rt△GCM中 ,所以Rt△DCM≌Rt△GCM(HL)所以CG=DC=4,MG=DM=2,
,所以Rt△DCM≌Rt△GCM(HL)所以CG=DC=4,MG=DM=2,
 ,化简,得8m=36,解得
,化简,得8m=36,解得 .
.
考点:1.待定系数法求函数解析式;2.抛物线的平移规律;3.全等三角形的判定与性质;4.角平分线的性质.

练习册系列答案
相关题目
 -
- =
=

 B.
B.  C.
C.  D.
D. 
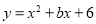 经过
经过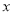 轴上两点
轴上两点 ,点
,点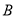 的坐标为
的坐标为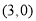 ,与
,与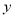 轴相交于点
轴相交于点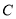 ;
;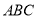 的面积;
的面积; 分别是△
分别是△ 的边
的边 和
和 上的点,
上的点, ,
, ,要使
,要使 ∥
∥ ,
, 应等于 ;
应等于 ;
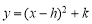 的形式.
的形式.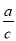 ; (B)tanA=
; (B)tanA=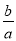 ; (C)sinA=
; (C)sinA=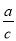 ; (D)cotA=
; (D)cotA=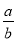 .
.