题目内容
P是⊙O的直径AB的延长线上一点,PC与⊙O相切于点C,∠APC的平分线交AC于Q,则∠PQC=分析:连接OC,由切线的性质得OC⊥PC,则∠OAC=∠OCA=
∠POC,再由已知条件求得∴∠PQC的度数.
| 1 |
| 2 |
解答: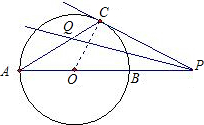 解:连接OC,
解:连接OC,
∵PC与⊙O相切于点C,
∴OC⊥PC,
∵OA=OC,
∴∠OAC=∠OCA=
∠POC,
又∵∠APQ=∠CPQ=
∠APC,
PAC+∠APQ,
=
(∠POC+∠APC),
=
×90°,
=45°.
故答案为45°.
 解:连接OC,
解:连接OC,∵PC与⊙O相切于点C,
∴OC⊥PC,
∵OA=OC,
∴∠OAC=∠OCA=
| 1 |
| 2 |
又∵∠APQ=∠CPQ=
| 1 |
| 2 |
PAC+∠APQ,
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=45°.
故答案为45°.
点评:本题考查了切线的性质,是基础知识比较简单.

练习册系列答案
相关题目
 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°. 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.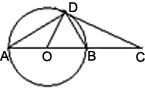 19、如图,C是⊙O的直径AB延长线上一点,过点C作⊙O的切线CD,D为切点,连接AD,OD,BD.请你根据图中所给出的已知条件(不再标注或使用其它字母,不再添加任何辅助线),写出两个你认为正确的结论:
19、如图,C是⊙O的直径AB延长线上一点,过点C作⊙O的切线CD,D为切点,连接AD,OD,BD.请你根据图中所给出的已知条件(不再标注或使用其它字母,不再添加任何辅助线),写出两个你认为正确的结论: 如图,AB是⊙O的直径,AF是弦,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
如图,AB是⊙O的直径,AF是弦,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.