题目内容
xl、x2是方程x2-2mx+（m2+2m+3）=O的两实根，则x12+x22的最小值是
______．
方程有实根，则△=4m2-4（m2+2m+3）=-8m-12≥0，
故m≤-
，
又有x1+x2=2m，x1•x2=m2+2m+3，
得x12+x22=（x1+x2）2-2x1•x2=2[（m-1）2-4]，
但m≤-
，
故当m≤-
时，x12+x22的最小值为2[（-
-1）2-4]=2×
=
．
故答案为：
．
故m≤-
| 3 |
| 2 |
又有x1+x2=2m，x1•x2=m2+2m+3，
得x12+x22=（x1+x2）2-2x1•x2=2[（m-1）2-4]，
但m≤-
| 3 |
| 2 |
故当m≤-
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 9 |
| 2 |
故答案为：
| 9 |
| 2 |
练习册系列答案
口算能手系列答案
相关题目
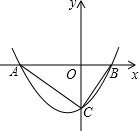3=0的两个根（x1＜x2），而且抛物线与y轴交于C点，∠ACB不小于90°
