题目内容
xl、x2是方程x2-2mx+(m2+2m+3)=O的两实根,则x12+x22的最小值是分析:先根据根的判别式求得m的取值范围,然后由根与系数的关系列出关于m的一元二次方程,最后由方程的性质解答.
解答:解:方程有实根,则△=4m2-4(m2+2m+3)=-8m-12≥0,
故m≤-
,
又有x1+x2=2m,x1•x2=m2+2m+3,
得x12+x22=(x1+x2)2-2x1•x2=2[(m-1)2-4],
但m≤-
,
故当m≤-
时,x12+x22的最小值为2[(-
-1)2-4]=2×
=
.
故答案为:
.
故m≤-
| 3 |
| 2 |
又有x1+x2=2m,x1•x2=m2+2m+3,
得x12+x22=(x1+x2)2-2x1•x2=2[(m-1)2-4],
但m≤-
| 3 |
| 2 |
故当m≤-
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 9 |
| 2 |
故答案为:
| 9 |
| 2 |
点评:本题主要考查了根与系数的关系、根的判别式及一元二次方程的最值.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
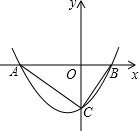 3=0的两个根(x1<x2),而且抛物线与y轴交于C点,∠ACB不小于90°
3=0的两个根(x1<x2),而且抛物线与y轴交于C点,∠ACB不小于90°