Question

【题目】如图所示，在中，，于点D，BE平分，且于点E与CD相交于点F，于点H，交BE于点G，下列结论：①；②；③④；其中正确的是___________．

Answer 1

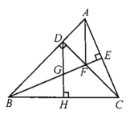
【答案】①②③④

【解析】

先根据AAS证明△ADC≌△FDB，得到AD=DF，∠DAC=∠DFB，从而得出①正确；

在Rt△ADF中，由AD=DF求得∠DFA，根据等腰直角三角形的性质求得∠HDC=，从而得到∠DFA=∠HDC，由平行线的判定得到④正确；

根据ASA证明△ABE≌△CBE，得到CE=AC，结合①中证明△ADC≌△FDB可得AC=BF，则得出③正确；

由等腰三角形的性质、角平分线的性质和三角形内角和定理求得∠DFB，由等腰三角形的性质、角平分线的性质和三角形外角性质求得∠DGF=，从而得到∠DFB=∠DGF，再由等角对等边得到②正确．

∵于点D，于点E，

∴∠BDF=∠BDA=,∠BAC+∠ABF=∠DAC+∠ACD=，

∴∠ABF=∠ACD，

在△ADC和△FDB中

，

∴△ADC≌△FDB（AAS），

∴AD=DF，∠DAC=∠DFB，

又∵DF+CF=CD，CD=BD，

∴，故①正确；

∵AD=DF，于点D，

∴∠DAF=∠DFA=，

∵BD=DC，于点D，于点H，

∴∠HDC=∠HDB=，

又∵∠DFA，

∴∠DFA=∠HDC，

∴，故④正确；

∵BE平分，且于点E，

∴∠ABE=∠CBE,∠AEB=∠CEB，

在△ABE和△CBE中

，

∴△ABE≌△CBE，

∴AE=CE，

∴CE=AC，

又∵△ADC≌△FDB，

∴BF=AC，

∴，故③正确；

∵，于点D，

∴∠DBC=,

又∵BE平分，

∴∠DBE=，

∴∠DFB=，

又∵∠HDB=，

∴∠DGF=∠DBG+∠BDG=+=，

∴∠DFB=∠DGF，

∴DG＝DF，故②正确．

故答案为：①②③④．