Question

【题目】一直角三角板的直角顶点在直线上，作射线三角板的各边和射线都处于直线的上方．

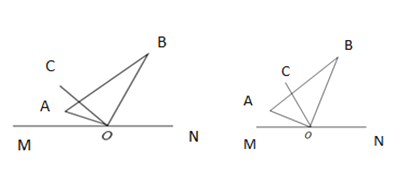
（1）将三角板绕点在平面内旋转，当平分时，如图1，如果，求的度数；

（2）如图2，将三角板绕点在平面内任意转动，如果始终在内，且，请问： 和有怎样的数量关系?

（3）如图2，如果平分，是否也平分?请说明理由．

Answer 1

【答案】（1）；（2）∠BOC－∠AOM＝；（3）OB平分∠CON．理由见解析

【解析】

（1）根据角平分线的意义可得∠COM=∠BOC=65°，再根据互余可求出∠AOC的度数；

（2）当OA始终在∠COM的内部时，有∠AOM+∠AOC=65°，∠AOC+∠BOC=90°，进而得出∠AOM与∠BOC的等量关系；

（3）根据余角的性质得出∠AOM+∠BOC=90°，再证明∠AOM+∠BON=90°，即可得出结论.

解：（1）∵平分，

∴∠COM=∠BOC=65°，

又∵∠AOC+∠BOC=90°，

∴∠AOC=90°-65°=25°；

（2）∵OA始终在∠COM的内部，

∠COM=∠AOM+∠AOC=65°，

∴∠AOC=65°-∠AOM，

又∵∠AOC+∠BOC=90°，

∴65°-∠AOM+∠BOC=90°，

∴∠BOC－∠AOM＝；

（3）∵平分，

∴∠AOM=∠AOC，

又∵∠AOC+∠BOC=90°，

∴∠AOM+∠BOC=90°，

∵∠AOB=90°，

∴∠AOM+∠BON=90°，

∴∠BOC=∠BON，

∴平分.