题目内容
如图，E是等边△ABC中AC边上的点，∠1=∠2，BE=CD，则对△ADE的形状最准确的判断是
- A.等腰三角形
- B.等边三角形
- C.不等边三角形
- D.不能确定形状
B
试题分析：先由△ABC为等边三角形，可得AB=AC，再有∠1=∠2，BE=CD，根据“SAS”证得△ABE≌△ACD，即得AE=AD，∠BAE=∠CAD=60°，从而可得△ADE是等边三角形．
∵△ABC为等边三角形
∴AB=AC
∵∠1=∠2，BE=CD
∴△ABE≌△ACD
∴AE=AD，∠BAE=∠CAD=60°
∴△ADE是等边三角形．
故选B．
考点：本题考查的是等边三角形的判定和性质，全等三角形的判定和性质
点评：解答本题的关键是证得△ABE≌△ACD，再结合有一个角为60°的等腰三角形是等边三角形。
试题分析：先由△ABC为等边三角形，可得AB=AC，再有∠1=∠2，BE=CD，根据“SAS”证得△ABE≌△ACD，即得AE=AD，∠BAE=∠CAD=60°，从而可得△ADE是等边三角形．
∵△ABC为等边三角形
∴AB=AC
∵∠1=∠2，BE=CD
∴△ABE≌△ACD
∴AE=AD，∠BAE=∠CAD=60°
∴△ADE是等边三角形．
故选B．
考点：本题考查的是等边三角形的判定和性质，全等三角形的判定和性质
点评：解答本题的关键是证得△ABE≌△ACD，再结合有一个角为60°的等腰三角形是等边三角形。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，△ABC是等边三角形，AB=4cm，则BC边上的高AD等于
如图，△ABC是等边三角形，点D是线段BC上的一个动点（点D不与点B、C重合），△ADE是以AD为边的等边三角形，过点E作BC的平行线，分别交AB、AC于点F、G，连接BE．
如图，△ABC是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E．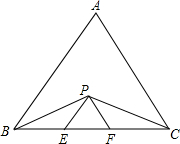
如图，△ABC是等边三角形，P为△ABC内任意一点，PE∥AB，PF∥AC．那么，△PEF是什么三角形？说明理由．