题目内容
 如图,△ABC是等边三角形,点D是线段BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,连接BE.
如图,△ABC是等边三角形,点D是线段BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,连接BE.(1)若△ABC的面积是1,则△ADE的最小面积为
| 3 |
| 4 |
| 3 |
| 4 |
(2)求证:△AEB≌ADC;
(3)探究四边形BCGE是怎样特殊的四边形?并说明理由.
分析:(1)根据题意得当AD最小时三角形AED的面积最小,当AD为BC边上的高时AD最短,首先求得AD的长然后求得面积即可;
(2)利用等边三角尺是性质得到AE=AD,AB=AC,∠EAD=∠BAC=60°,然后得到∠EAB=∠DAC,从而证明两个三角形全等;
(3)根据全等三角形得到∠ABE=∠BAC,从而得到EB∥GC.再根据EG∥BC判定四边形BCGE是平行四边形即可.
(2)利用等边三角尺是性质得到AE=AD,AB=AC,∠EAD=∠BAC=60°,然后得到∠EAB=∠DAC,从而证明两个三角形全等;
(3)根据全等三角形得到∠ABE=∠BAC,从而得到EB∥GC.再根据EG∥BC判定四边形BCGE是平行四边形即可.
解答:证明:(1)由题意得当AD⊥BC时,AD最小;
此时AD:AB=
:2
∵△ABC的面积是1,
∴△ADE的最小面积为
;
(2)∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°.(1分)
又∵∠EAB=∠EAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠EAB=∠DAC,
∴△AEB≌△ADC.(3分)
(3)方法一:由①得△AEB≌△ADC,
∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABE=∠BAC,
∴EB∥GC.(5分)
又∵EG∥BC,
∴四边形BCGE是平行四边形.(6分)
方法二:证出△AEG≌△ADB,得EG=AB=BC.(5分)
由①得△AEB≌△ADC.得BE=CG.
∴四边形BCGE是平行四边形.(6分)
此时AD:AB=
| 3 |
∵△ABC的面积是1,
∴△ADE的最小面积为
| 3 |
| 4 |
(2)∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°.(1分)
又∵∠EAB=∠EAD-∠BAD,∠DAC=∠BAC-∠BAD,
∴∠EAB=∠DAC,
∴△AEB≌△ADC.(3分)
(3)方法一:由①得△AEB≌△ADC,
∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABE=∠BAC,
∴EB∥GC.(5分)
又∵EG∥BC,
∴四边形BCGE是平行四边形.(6分)
方法二:证出△AEG≌△ADB,得EG=AB=BC.(5分)
由①得△AEB≌△ADC.得BE=CG.
∴四边形BCGE是平行四边形.(6分)
点评:本题考查了等边三角形的性质、全等三角形的性质与判定及平行四边形的判定,考查的知识点比较多,但难度不算很大.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
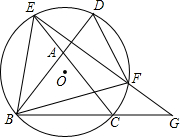 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.