题目内容
【题目】如图,在平面直角坐标系中有一边长为l的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OBl为边作第三个正方形OBlB2C2,照此规律作下去,则点B2020的坐标为__________.

【答案】(-21010,-21010)
【解析】
根据正方形的性质找出部分点Bn的坐标,由坐标的变化找出变化规律“B8n+1(0,24n+1),B8n+2(-24n+1,24n+1),B8n+3(-24n+2,0),B8n+4(-24n+2,-24n+2),B8n+5(0,-24n+3),B8n+6(24n+3,-24n+3),B8n+7(24n+4,0),B8n+8(24n+4,24n+4)”,依此规律即可得出结论.
解:观察,发现规律:B1(0,2),B2(-2,2),B3(-4,0),B4(-4,-4),B5(0,-8),B6(8,-8),B7(16,0),B8(16,16),B9(0,32),
∴B8n+1(0,24n+1),B8n+2(-24n+1,24n+1),B8n+3(-24n+2,0),B8n+4(-24n+2,-24n+2),B8n+5(0,-24n+3),B8n+6(24n+3,-24n+3),B8n+7(24n+4,0),B8n+8(24n+4,24n+4).
∵2020=8×252+4,
∴B2020(-21010,-21010).
故答案为:(-21010,-21010).

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
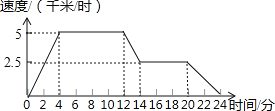
【题目】某天放学后,小敏徒步回家,如图所示,反映了她的速度与时间的变化关系.
(1)请你根据图象填写下表:
时间/分 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 24 |
速度/(千米/时) |
(2)根据图象或表格你能叙述一下小敏行走的情况吗?