题目内容
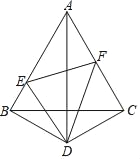
【题目】如图,直线![]() 交y轴于点C,交x轴于点D,直线
交y轴于点C,交x轴于点D,直线![]() 经过点A(4,0),且两直线交于点B(2,m).
经过点A(4,0),且两直线交于点B(2,m).

(1)求m的值和直线![]() 的函数表达式;
的函数表达式;
(2)直线![]() 在第一象限内的部分有一点E,且
在第一象限内的部分有一点E,且![]() ,求出点E的坐标,并在y轴上找一点P,使得BP+PE的值最小,求出P的坐标和这个最小值;
,求出点E的坐标,并在y轴上找一点P,使得BP+PE的值最小,求出P的坐标和这个最小值;
(3)在(2)的条件下,若点Q为y轴上一点,且△BPQ为等腰三角形,请直接写出点Q的坐标.
【答案】(1)![]() ,
,![]() ;(2)E(6,2) ,P(0,-1),最小值为:
;(2)E(6,2) ,P(0,-1),最小值为:![]() ;(3)点Q的坐标为
;(3)点Q的坐标为![]() 或
或![]() 或(0,-3)或(0,
或(0,-3)或(0,![]() ).
).
【解析】
(1)首先易求m的值,得到B点坐标,然后用待定系数法求直线![]() 的函数表达式即可;
的函数表达式即可;
(2)求出D(1,0),得出AD=3,根据![]() 且点E在第一象限内的直线
且点E在第一象限内的直线![]() 上,可得E点纵坐标为2,进而得到E(6,2),作点B(2,-2)关于y轴的对称点B1(-2,-2),连接B1E交y轴于点P,此时B1P+PE最小,用两点间距离公式可求这个最小值,然后再用待定系数法求出直线B1E的解析式,进而可得P的坐标;
上,可得E点纵坐标为2,进而得到E(6,2),作点B(2,-2)关于y轴的对称点B1(-2,-2),连接B1E交y轴于点P,此时B1P+PE最小,用两点间距离公式可求这个最小值,然后再用待定系数法求出直线B1E的解析式,进而可得P的坐标;
(3)分三种情况:①当BP=PQ时,求出BP,即可得到点Q坐标;②当BP=BQ时,则点B在线段PQ的垂直平分线上,进而得到点Q坐标;③当BQ=PQ时,可根据两点间距离公式列方程求出点Q坐标.
解:(1)∵点B(2,m)在直线![]() 上,
上,
∴![]() ,
,
∴B(2,-2),
设直线![]() ,
,
∵A(4,0),B(2,-2)在直线![]() 上,
上,
∴![]() ,解得:
,解得:![]() ,
,
∴直线![]() 的函数表达式为:
的函数表达式为:![]() ;
;
(2)令-2x+2=0,解得 x=1,
∴D(1,0),
∵A(4,0),B(2,-2),
∴AD=3,
由条件设E(a,b),
∵![]() ,
,
∴![]() ,
,
∵E(a,b)在第一象限内的直线![]() 上,
上,
∴b=2,
∴a=6,即E(6,2) ,
作点B(2,-2)关于y轴的对称点B1(-2,-2),连接B1E交y轴于点P,此时BP+PE最小,
最小值为![]() ,
,
设直线B1E的解析式为y=kx+b,
则![]() ,解得:
,解得: ,
,
∴直线B1E的解析式为![]() ,
,
当x=0时,y=-1,
∴P(0,-1);

(3)由题意得:B(2,-2),P(0,-1),△BPQ为等腰三角形,
①当BP=PQ时,
∵![]() ,
,
∴点Q纵坐标为![]() 或
或![]() ,
,
∴点Q坐标为:![]() 或
或![]() ;
;
②当BP=BQ时,则点B在线段PQ的垂直平分线上,易得点Q纵坐标为-3,
∴点Q坐标为:(0,-3);
③当BQ=PQ时,设点Q坐标为(0,n),
则![]() ,
,
解得:![]() ,
,
∴点Q坐标为:(0,![]() ),
),
综上所述,满足条件的点Q的坐标为![]() 或
或![]() 或(0,-3)或(0,
或(0,-3)或(0,![]() ).
).

 名校课堂系列答案
名校课堂系列答案