题目内容
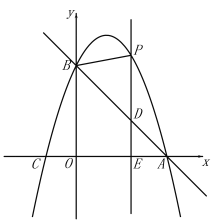
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过A,B.
经过A,B.
(1)求抛物线解析式;
(2)E(m,0)是x轴上一动点,过点E作![]() 轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
①点E在线段OA上运动,若△PBD是等腰三角形时,求点E的坐标;
②点E在x轴的正半轴上运动,若![]() ,请直接写出m的值.
,请直接写出m的值.
【答案】(1)![]() ;(2)①点E的坐标为
;(2)①点E的坐标为![]() ,
,![]() 或
或![]() ;②m的值为
;②m的值为![]() 或5
或5
【解析】
(1)把![]() 代入
代入![]() ,求出点B的坐标,再把
,求出点B的坐标,再把![]() 代入
代入![]() ,求出b,c的值即可;
,求出b,c的值即可;
(2)先求出![]() ,①分
,①分![]() ,
,![]() ,
,![]() 三种情况分析即可;②先求出直线BC的解析式,当点P在x轴上方时,
三种情况分析即可;②先求出直线BC的解析式,当点P在x轴上方时,![]() ,可得出直线BP的解析式为:
,可得出直线BP的解析式为:![]() ,求出与抛物线的交点即可;当点P在x轴下方时,可得出直线BP的解析式为:
,求出与抛物线的交点即可;当点P在x轴下方时,可得出直线BP的解析式为:![]() ,求出与抛物线的交点即可.
,求出与抛物线的交点即可.
解:(1)把![]() 代入
代入![]() 得:
得:![]()
则B的坐标为![]() ,
,
把![]() 代入
代入![]() 中
中
得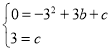
解得:![]()
∴抛物线的解析式的为:![]() .
.
(2) ∵![]()
∴![]()
又![]() 轴
轴
∴![]()
∴![]()
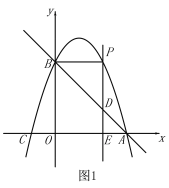
① 当![]() 时,如图1,
时,如图1,
∵△PBD是等腰直角三角形,
∴![]()
解得:![]() ;
;
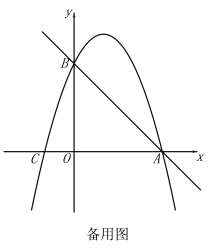
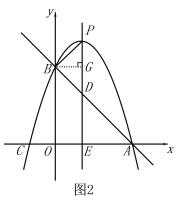
当![]() 时,如图2,
时,如图2,
过点B作BG⊥PD,△PBD是等腰直角三角形,
∴![]() .
.
∴![]() ,
,
解得:![]() ;
;
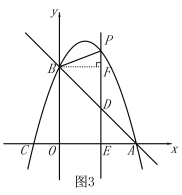
当![]() 时,如图3,
时,如图3,
过点B作BF⊥PD,△BFD是等腰直角三角形,
∴![]() .
.
∴![]() ,
,
解得:![]() ;
;
综上所述,点E的坐标为![]() ,
,![]() 或
或![]() .
.
② 根据抛物线解析式可得出点![]()
∴直线CB的解析式为:![]()
当点P在x轴上方时,如图1,
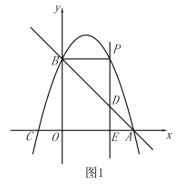
∵![]() ,
,![]()
∴![]()
∴直线BP的解析式为:![]()
∴![]()
解得:![]() (舍去)
(舍去)
当点P在x轴下方时,如下图所示:

∵![]() ,
,![]()
∴![]()
∴![]()
∴直线BP的解析式为:![]()
∴![]()
解得:![]() (舍去)
(舍去)
∴m的值为![]() 或5.
或5.

【题目】某校为了调查学生对卫生健康知识,特别是疫情防控下的卫生常识的了解,现从九年级![]() 名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
组别 | 成绩 | 人数 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|

请结合图表信息完成下列各题.
(1)表中a的值为_____,b的值为______;在扇形统计图中,第![]() 组所在扇形的圆心角度数为______°;
组所在扇形的圆心角度数为______°;
(2)若测试成绩不低于![]() 分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
(3)若测试成绩在![]() 分以上(含
分以上(含![]() 分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.
分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.