题目内容
【题目】在平面直角坐标系中,![]() 为原点,已知直线
为原点,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
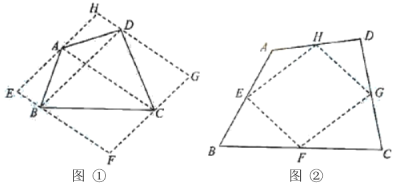
关于![]() 轴对称,如图①.
轴对称,如图①.
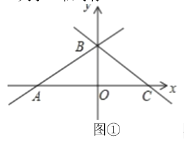
(1)点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,直线
的坐标为________,直线![]() 的解析式为________.
的解析式为________.
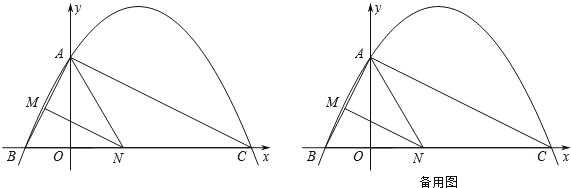
(2)点![]() 是
是![]() 轴上的一个动点(点
轴上的一个动点(点![]() 不与点
不与点![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() .交直线
.交直线![]() 于点
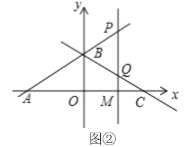
于点![]() (图②).
(图②).
①如图②,当点![]() 在
在![]() 轴的正半轴上时,若
轴的正半轴上时,若![]() 的面积为
的面积为![]() ,求点
,求点![]() 的坐标;
的坐标;
②连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②点P的坐标为
;②点P的坐标为![]() 或(
或(![]()
【解析】
(1)依据坐标轴上点的坐标特点可求得A、B的坐标,然后利用对称性可得到点C的坐标,接下来,利用待定系数法可求得BC的解析式;
(2)过点B作BD⊥PQ,垂足为D,先用含x的式子表示出PQ、BD的长,再用三角形面积公式进行计算即可;
(3)分情况讨论:①当点![]() 在
在![]() 轴的正半轴上时,先证明∠BAO=∠OBM,可得
轴的正半轴上时,先证明∠BAO=∠OBM,可得![]() ,根据相似三角形的性质求出OM的长,即可得点P的横坐标,然后将点P的横坐标代入函数解析式可求得点P的坐标;②当点
,根据相似三角形的性质求出OM的长,即可得点P的横坐标,然后将点P的横坐标代入函数解析式可求得点P的坐标;②当点![]() 在
在![]() 轴的负半轴上时,同理求解即可.
轴的负半轴上时,同理求解即可.
解:(1)对于![]() ,由
,由![]() 得:
得:![]() ,
,
∴![]() ,
,
由![]() 得:
得:![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∵点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
∴![]() ,
,
设直线![]() 的函数解析式为
的函数解析式为![]() ,
,
则:![]() ,解得
,解得
∴直线BC的函数解析式为![]() ,
,
故答案为:![]()
![]() ;
;
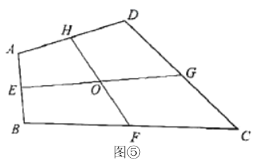
(2)如图所示:过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,

设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 的面积为
的面积为![]() ,
,
∴![]() ,
,
解得:![]() (负值舍去),
(负值舍去),
∴![]() ;
;
(3)分情况讨论:
①如图所示:当点![]() 在
在![]() 轴的正半轴上时.
轴的正半轴上时.

∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴![]() ;
;
②如图所示:当点![]() 在
在![]() 轴的负半轴上时,
轴的负半轴上时,

同理可得:![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴![]() ,
,
综上所述,点P的坐标为![]() 或
或![]() .
.

【题目】商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p= ,且其日销售量y(kg)与时间t(天)的关系如表:
,且其日销售量y(kg)与时间t(天)的关系如表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?