题目内容
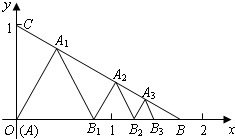
如图所示,已知第一个三角形周长为1,依次取三角形三边中点画三角形,在第n个图形中,最小三角形的周长是
分析:每个三角形的边都是前一个三角形的边的中点的两线,因而两个三角形相似,前一个图形中的最小的三角形与后一个图象中的最小三角形的相似比是1:2,则周长的比是
,第一个三角形的周长是1,则第二个是
,第三个是(
)2,同理第四个是(
)3,以此类推,在第n个图形中,最小的三角形的周长是(
)n-1.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:每个三角形的边都是前一个三角形的边的中点的两线,因而两个三角形相似,
前一个图形中的最小的三角形与后一个图象中的最小三角形的相似比是1:2,
则周长的比是
,
第一个三角形的周长是1,则第二个是
,第三个是(
)2,同理第四个是(
)3,
以此类推,在第n个图形中,最小的三角形的周长是(
)n-1.
故答案为:(
)n-1.
前一个图形中的最小的三角形与后一个图象中的最小三角形的相似比是1:2,
则周长的比是
| 1 |
| 2 |
第一个三角形的周长是1,则第二个是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
以此类推,在第n个图形中,最小的三角形的周长是(
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题主要考查了相似三角形的性质,周长的比等于相似比.找到规律是关键.

练习册系列答案
相关题目
 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质: 如图所示,已知:点A(0,0),B(
如图所示,已知:点A(0,0),B(
 如图所示,已知:点A(0,0),B(
如图所示,已知:点A(0,0),B(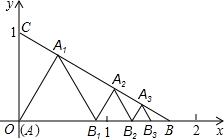 如图所示,已知直线
如图所示,已知直线